Next: Estimating Matching Quality
Up: Evaluating the Match
Previous: Evaluating the Match
In addition to subsampling, goals of competitive object learning
are the minimization of the expected quantization error and
entropy maximization. A finite set of 3D scan points 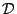 is
subsambled to the set
is
subsambled to the set
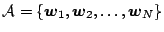 . Error minimization is done with respect to the following
function:
. Error minimization is done with respect to the following
function:
with the set 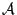 of samples and the Voronoi
set
of samples and the Voronoi
set
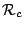 of unit
of unit 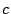 , i.e.,
, i.e.,
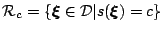 and
and
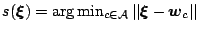 . Entropy maximization guarantees inherent
robustness. The failure of reference vectors, i.e., missing 3D
points, affects only a limited fraction of the data. Interpreting
the generation of an input signal and the subsequent mapping onto
the nearest sample in
. Entropy maximization guarantees inherent
robustness. The failure of reference vectors, i.e., missing 3D
points, affects only a limited fraction of the data. Interpreting
the generation of an input signal and the subsequent mapping onto
the nearest sample in 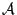 as a random experiment which
assigns a value
as a random experiment which
assigns a value
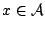 to the random variable
to the random variable 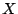 , then
maximizing the entropy
, then
maximizing the entropy
is equivalent to equiprobable samples. The following neural gas
algorithm learns and subsamples 3D points clouds [7]:
- i.).
- Initialize the set
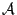 to contain
to contain 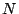 vectors, randomly
from the input set. Set
vectors, randomly
from the input set. Set 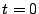 .
.
- ii.).
- Generate at random an input element
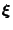 , i.e., select a
point from
, i.e., select a
point from 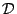 .
.
- iii.).
- Order all elements of
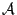 according to their distance to
according to their distance to
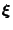 , i.e., find the sequence of indices
, i.e., find the sequence of indices
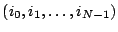 such that
such that
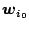 is the reference
vector closest to
is the reference
vector closest to 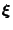 ,
,
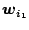 is the reference
vector second closest to
is the reference
vector second closest to 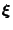 , etc.,
, etc.,
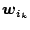 ,
,
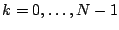 is the reference vector such that
is the reference vector such that 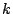 vectors
vectors 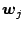 exists that are closer to
exists that are closer to 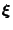 than
than
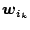 .
.
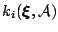 denotes the number
denotes the number 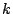 associated with
associated with
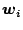 .
.
- iv.).
- Adapt the reference vectors according to
with the following time dependencies:
- v.).
- Increase the time parameter
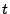 .
.
The neural gas algorithms is used with the following parameters:
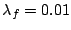 ,
,
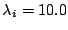 ,
,
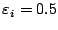 ,
,
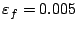 ,
,
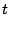 max
max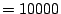 . Note that
. Note that
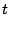 max controls the run time. Fig.
max controls the run time. Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) shows 3D models of the database (top row) and subsampled versions
(bottom) with 250 points.
shows 3D models of the database (top row) and subsampled versions
(bottom) with 250 points.
Figure:
Top: 3D models (point clouds) of the database. Bottom:
sumbsampled models with 250 points.
|
|



Next: Estimating Matching Quality
Up: Evaluating the Match
Previous: Evaluating the Match
root
2005-05-03
![]() is
subsambled to the set
is
subsambled to the set
![]() . Error minimization is done with respect to the following
function:
. Error minimization is done with respect to the following
function: