


Next: Approximate box decomposition trees
Up: Approximate Data Association
Previous: Approximate Data Association
Since the ICP algorithm, and therefore our 6D SLAM method,
extensively computes nearest neigbours, approximating the nearest
neigbours will speed up the algorithm. S. Arya and D. Mount
introduce the following notion for approximating the nearest
neighbor [3]: Given an 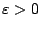 , then the point
, then the point
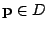 is the
is the
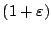 -approximate nearest neighbour of
the point
-approximate nearest neighbour of
the point 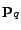 , iff
, iff
where 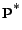 denotes the true nearest neighbour, i.e.,
denotes the true nearest neighbour, i.e., 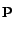 has a maximal distance of
has a maximal distance of 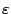 to the true nearest
neighbour. Using this notation in every step the algorithm
records the closest point
to the true nearest
neighbour. Using this notation in every step the algorithm
records the closest point 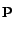 . The search terminates if the
distance to the unanalyzed leaves is larger than
Fig.
. The search terminates if the
distance to the unanalyzed leaves is larger than
Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) (left) shows an example where the gray
cell needs not to be analyzed, since the point
(left) shows an example where the gray
cell needs not to be analyzed, since the point 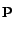 satisfies
the approximation criterion.
satisfies
the approximation criterion.
root
2005-05-03
![]() , then the point
, then the point
![]() is the
is the
![]() -approximate nearest neighbour of
the point
-approximate nearest neighbour of
the point ![]() , iff
, iff