


Next: ICP-based 6D SLAM
Up: Range Image Registration and
Previous: Range Image Registration and
In every iteration the optimal tranformation (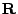 ,
, 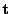 )
has to be computed. Eq. (
)
has to be computed. Eq. (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) can be reduced to
) can be reduced to
with
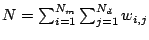 , since the
correspondence matix can be represented by a vector containing
the point pairs.
, since the
correspondence matix can be represented by a vector containing
the point pairs.
Four methods are known to minimize eq. (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
[17]. In earlier work [20,27] we
used a quaternion based method [7], but the
following one, based on singular value decomposition (SVD), is
robust and easy to implement, thus we give a brief overview of
the SVD-based algorithms. It was first published by Arun, Huang
and Blostein [2]. The difficulty of this
minimization problem is to enforce the orthonormality of matrix
)
[17]. In earlier work [20,27] we
used a quaternion based method [7], but the
following one, based on singular value decomposition (SVD), is
robust and easy to implement, thus we give a brief overview of
the SVD-based algorithms. It was first published by Arun, Huang
and Blostein [2]. The difficulty of this
minimization problem is to enforce the orthonormality of matrix
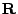 . The first step of the computation is to decouple the
calculation of the rotation
. The first step of the computation is to decouple the
calculation of the rotation 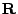 from the translation
from the translation 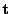 using the centroids of the points belonging to the matching,
i.e.,
using the centroids of the points belonging to the matching,
i.e.,
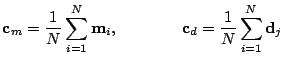 |
|
|
(3) |
and
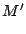 |
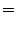 |
|
(4) |
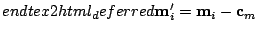 |
|
|
(5) |
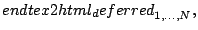 |
|
|
(6) |
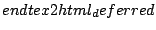 |
|
|
(7) |
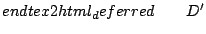 |
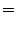 |
|
(8) |
 |
|
|
(9) |
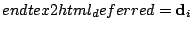 |
|
|
(10) |
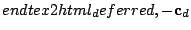 |
|
|
(11) |
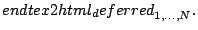 |
|
|
(12) |
After replacing (![[*]](file:/usr/share/latex2html/icons/crossref.png) ), (
), (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and
(
) and
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ) in the error function,
) in the error function,
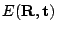 eq. (
eq. (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) becomes:
) becomes:
In order to minimize the sum above, all terms have to be
minimized. The second sum (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is zero, since all
values refer to centroid. The third part (
) is zero, since all
values refer to centroid. The third part (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) has
its minimum for
) has
its minimum for
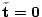 or
or
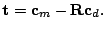 |
|
|
(14) |
Therefore the algorithm has to minimize only the first
term, and the error function is expressed in terms of the
rotation only:
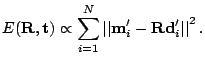 |
|
|
(15) |
Theorem: The optimal rotation is calculated
by
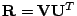 . Herby the matrices
. Herby the matrices 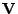 and
and 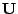 are
derived by the singular value decomposition
are
derived by the singular value decomposition
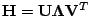 of a correlation matrix
of a correlation matrix 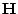 . This
. This
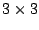 matrix
matrix
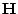 is given by
is given by
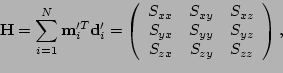 |
|
|
(16) |
with
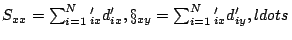 . The analogous
algorithm is derived directly from this theorem.
. The analogous
algorithm is derived directly from this theorem.
Proof: Since rotation is length preserving, i.e.,
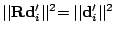 the error function (
the error function (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) is expanded
) is expanded
The rotation affects only the middle term, thus it is sufficient
to maximize
Using the trace of a matrix, (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) can be rewritten to
obtain
) can be rewritten to
obtain
With 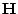 defined as in (
defined as in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ). Now we have
to find the matrix
). Now we have
to find the matrix 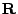 that maximizes
that maximizes
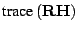 .
.
Assume that the singular value decomposition of 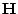 is
is
with 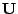 and
and 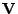 orthonormal
orthonormal
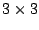 matrices and
matrices and
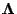 a
a
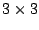 diagonal matrix without negative
elements. Suppose
diagonal matrix without negative
elements. Suppose
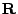 is orthonormal and
is orthonormal and
is a symmetric, positive definite matrix. Arun, Huang and
Blostein provide a lemma to show that
for any orthonormal matrix 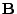 . Therefore the matrix
. Therefore the matrix 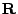 is
optimal. Prooving the lemma is straightforward using the
Cauchy-Schwarz [2]. Finally, the
optimal translation is calculated as (cf. eq. (
is
optimal. Prooving the lemma is straightforward using the
Cauchy-Schwarz [2]. Finally, the
optimal translation is calculated as (cf. eq. (![[*]](file:/usr/share/latex2html/icons/crossref.png) )
and (
)
and (![[*]](file:/usr/share/latex2html/icons/crossref.png) ))
))



Next: ICP-based 6D SLAM
Up: Range Image Registration and
Previous: Range Image Registration and
root
2005-05-03
![]() ,
, ![]() )
has to be computed. Eq. (
)
has to be computed. Eq. (![]() ) can be reduced to
) can be reduced to
![]() )
[17]. In earlier work [20,27] we
used a quaternion based method [7], but the
following one, based on singular value decomposition (SVD), is
robust and easy to implement, thus we give a brief overview of
the SVD-based algorithms. It was first published by Arun, Huang
and Blostein [2]. The difficulty of this
minimization problem is to enforce the orthonormality of matrix
)
[17]. In earlier work [20,27] we
used a quaternion based method [7], but the
following one, based on singular value decomposition (SVD), is
robust and easy to implement, thus we give a brief overview of
the SVD-based algorithms. It was first published by Arun, Huang
and Blostein [2]. The difficulty of this
minimization problem is to enforce the orthonormality of matrix
![]() . The first step of the computation is to decouple the
calculation of the rotation
. The first step of the computation is to decouple the
calculation of the rotation ![]() from the translation
from the translation ![]() using the centroids of the points belonging to the matching,
i.e.,
using the centroids of the points belonging to the matching,
i.e.,
![]() ), (
), (![]() ) and
(
) and
(![]() ) in the error function,
) in the error function,
![]() eq. (
eq. (![]() ) becomes:
) becomes:
![]() . Herby the matrices
. Herby the matrices ![]() and
and ![]() are
derived by the singular value decomposition
are
derived by the singular value decomposition
![]() of a correlation matrix
of a correlation matrix ![]() . This
. This
![]() matrix
matrix
![]() is given by
is given by
![]() the error function (
the error function (![]() ) is expanded
) is expanded
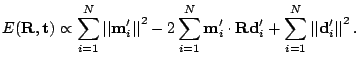
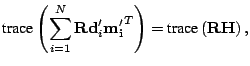
![]() is
is