In this paper, we have achieved this using linear image filters to detect the edges in the image, followed by a threshold to eliminate noise data, which would then be given as input to the classifier, which in turn handles differences in size, pattern, lighting, etc.
The most common edge detection techniques used are gradient and Laplacian operators. For this paper, we have experimented with multiple gradient filters, as well as a Laplacian filter, which we implemented ourselves, according to the algorithm described in [3]. The technique of the gradient operator is defined as follows:

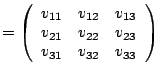 |
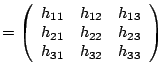 |
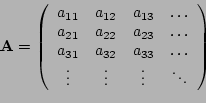
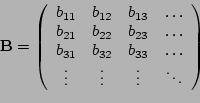
where ![]() represents the matrix of pixels in the input
image,
represents the matrix of pixels in the input
image, ![]() the output image and
the output image and ![]() and
and ![]() the
the ![]() vertical
and horizontal masks that are moved over the image pixels starting at
the top left corner, through to the bottom right. A number of
parameters need to be adjusted for each filter instance, such as the
vertical
and horizontal masks that are moved over the image pixels starting at
the top left corner, through to the bottom right. A number of
parameters need to be adjusted for each filter instance, such as the
![]() , which defines how ``thick'' the output edges should
be, and
, which defines how ``thick'' the output edges should
be, and ![]() and
and ![]() to emphasize the differentiation
in each direction (horizontal or vertical, respectively).
to emphasize the differentiation
in each direction (horizontal or vertical, respectively).
In our approach, we used a Sobel filter, with ![]() and
and ![]() defined
below,
defined
below,
![]() and both
and both ![]() and
and ![]() equal to
equal to ![]() .
.
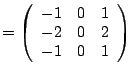 |
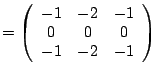 |
Two techniques were attempted in terms of filtering and thresholding:
![\includegraphics[width=43mm]{prewittOld}](img36.png)
![\includegraphics[width=43mm]{prewittNew}](img37.png)
|
This edge detection and thresholding technique is applied to all images used as input to the training of the Haar classifier. The training process itself is illustrated in the following subsections.