


Next: Merging Ground Points into
Up: Surface Extraction
Previous: Surface Extraction
Based on the idea by Wulf et al. [32] we have
designed an algorithm for labeling floor points in 3D scans. This
is done by computing the gradient between a point
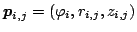 , given in a cylindrical coordinate
system, and its
, given in a cylindrical coordinate
system, and its 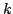 -th neighbor in measurement order within the
vertical sweep plane, i.e., a search region around
-th neighbor in measurement order within the
vertical sweep plane, i.e., a search region around 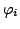 ,
according to the following equation (cf.. 3
middle, vertical cylindrical coordinate system):
,
according to the following equation (cf.. 3
middle, vertical cylindrical coordinate system):
with
In comparison with a fixed threshold 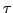 (here:
(here:
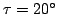 ), each 3D point is assigned to one of the following
three groups, which has proved to be robust against uneven and
non-horizontal ground:
), each 3D point is assigned to one of the following
three groups, which has proved to be robust against uneven and
non-horizontal ground:
1. ¯
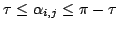 : ¯
: ¯
1.
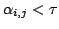 :
:
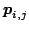 is aground point
is aground point
2.
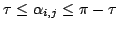 :
:
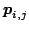 is an objectpoint
is an objectpoint
3.
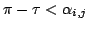 :
:
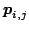 is a ceiling point
is a ceiling point
Figure:
Left: 3D scan planes due to the rotation of the 2D
laser range finder vs. 3D sweep planes. Right: Interpretation
example: One vertical sweep plane.
|
|
A result of the ground segmentation is displayed in
Fig. 4. The classification of a scan point as
``ground'' based on its neighborhood instead of performing a
simple height comparison is essential due to potential inaccuracy
in the scanner mount calibration and unknown starting pose, namely, the
pitch angle of the robot, as well as the significant unevenness
of the terrain.
Absolute height values of points do come into play when nearby drivable surface
points are to be merged into one large drivable area. Our point classification
scheme leaves the possibility open that two nearby points in a 3D model are both
correctly labeled ground, but are of significant difference in absolute height,
such as on the two horizontal neighborhoods of a vertical cliff. This needs to be
checked when growing neighboring ground points to drivable surfaces, as
described next.
Figure 4:
Left: A single outdoor 3D scan of a gravel path
in the Botanical Garden. Note that the path is uneven.
Middle: Areas (triangles) between neighboring surface
points all labeled drivable are shaded in blue. Note first that
the area in front is very dense with surface points, which are
all labeled drivable. Note second that there are some
disconnected patches of surface points in and behind the path
shoulder. Right: View into the model from the same
virtual view point as before, but with the next scans along the
path registered. Sufficiently large areas sufficiently dense
with drivable surface points are filled with blue. (Again, the
area in front is completely drivable.) Note that the next scan
has been taken too far away from the one in front to connect
the drivable surface areas, so some of the objectively drivable
path remains unlabeled here for lack of point density.
|
|



Next: Merging Ground Points into
Up: Surface Extraction
Previous: Surface Extraction
root
2006-03-16
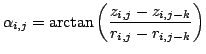
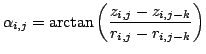
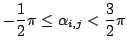
: ¯
:
is aground point
:
is an objectpoint
:
is a ceiling point
![\includegraphics[width=0.5\linewidth]{sweepplanes}](img85.png)
![\includegraphics[width=0.32\linewidth]{vertical}](img86.png)
![\fbox{\includegraphics[width=0.3\linewidth]{a2}}](img87.png)
![\fbox{\includegraphics[width=0.3\linewidth]{a1}}](img88.png)
![\fbox{\includegraphics[width=0.3\linewidth]{b2}}](img89.png)