Fast acquiring and analysis of three dimensional laser range data

Hartmut Surmann, Kai Lingemann, Andreas Nüchter and Joachim Hertzberg

FhG AiS - Fraunhofer Gesellschaft
Institute for Autonomous intelligent Systems, Schloss Birlinghoven,
D-53754 Sankt Augustin, Germany, {surmann $\vert$ lingemann $\vert$ nuechter $\vert$ hertzberg}@ais.fraunhofer.de
VMV 2001, Stuttgart, 21 - 23 Nov. 2001

Abstract:

This paper presents a precise ( $\approx$ 1cm), lightweight (5kg) and low cost 3D laser range finder for the fast gaging (

sec) of environments. Real-time algorithms for the data reduction, 3D-object segmentation are also presented. A special designed suspension unit, a standard servo motor and a standard 2D range finder are used to build the 3D scanner. Maximal resolutions e.g. 180 (h) $\times$ 90 (v) degree with 194400 points are grabbed in 8.1 seconds and low resolutions with 16200 points are grabbed in 1.4 seconds. While scanning, different online algorithms for line and surface detection are applied to the data. 3D-Object segmentation and detection are done offline after the scan. With the proposed approach, a precise, reliable, mobile, low cost, and real-time capable 3D sensor for the contact-less measuring of environments without additional landmarks is available.

Introduction

Range image acquisition can be defined as the process of determining the distance (or depth) from a given observation point to all points of consideration in a scene. The technology of laser range finders is not new and has been used for many years in military and airborne remote sensing survey applications. Many systems are available for a wide range of applications, for example land surveying, quality control, and civil engineering.

An important issue for man made environments is the choice of the sensor type from which raw range information from the scene is obtained. Today's commercial 3D laser range finders are large and heavy, build for stationary use mainly.

This paper presents a mobile 3D laser range finder. (fig. 1). The scanner is built on the base of a commercial 2D laser range finder from Schmersal together with a special designed suspension unit and a standard servo motor1 (1). The 2D scanner is very fast (processing time $\sim$ 15 ms), precise ( $\sim$ 1 cm, $180^{\circ}$ ) and becoming cheaper ( $\sim$ $3000) since different competing products e.g. 3 (3); 2 (2) are available.

**Figure 1:** The 3D laser range finder. The servo is mounted at the left side.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {3d-laser.eps}\end{center}\end{figure}$

A few number of scientific groups develop fast, lightweight and mobile 3D laser range finders and/or special algorithms on the basis of 2D laser range finders to overcome the drawback of only 2D proximity information 7 (7); 6 (6); 5 (5); 4 (4). Thrun et al. use two laser range finders, one rotated by 90 degrees 5 (5). The 3D information is generated while the robot is moving. The accuracy of the acquired data depends on the accuracy of the robot pose. 3D-Object detection without moving the robot is not possible. Waltheim et al. 7 (7) and Kristensen et al. 6 (6) use an amtec rotation module 8 (8) with high accuracy at high costs ( $\sim$ $3500).

Architecture of the 3D laser range finder

The presented 3D laser range finder is built on the basis of a 2D range finder by extension with a mount and a servomotor. The 2D laser range finder is attached to the mount for being rotated. The rotation axis is horizontal. A standard servo ( $\sim$ $75) is connected on the left side (fig. 1). Annotation: An alternative approach is to rotate the range finder around the vertical axis. Throughout this paper we will only discuss the approach based on a horizontal rotation, all presented algorithms can be used in the same way. The differences between both approaches are the orientation of the apex angle and the effects of dynamic objects moving through the scene, e.g. persons. Using vertical scanning, a perturbation either appears with low probability within a few scans making them useless for further data processing, or does not appear at all. The first approach on the other hand shows perturbations throughout the whole scene, but these data can still be used for robot navigation and object detection.

Due to the flexible setup we can connect different 2D laser range finders (Schmersal 3 (3), Sick 2 (2)). This leads to a wide variety of scan resolutions and scan speeds (see tab. 1) - the latter also depending on the used serial device. The used laser range finder (max. scanning distance 60m) can also be used outside of buildings (see fig.2).

Table 1: Comparison between Schmersal 3 (3) and Sick 2 (2) laser scanner, connected to two different serial devices.

		Schmersal	Sick
points	low	11250	16200
	maximal	135000	194400
RS232	low	5.4 sec	5.6 sec
	maximal	48 sec	67.5 sec
RS422	low	5.4 sec	1.35 sec
	maximal	16.2 sec	8.1 sec
resolution (hor.)	5 cm	1 cm
resolution (rot.)	1 $^{\circ}$	1 $^{\circ}$

The given setup determines an intrinsic order of the acquired data. The data coming from the 2D laser range finder is ordered anticlockwise. In addition the 2D scans (scanned planes) are ordered due to the rotation.

The 3D laser range finder uses only standard computer interfaces. The servomotor is directly connected to the parallel port, the 2D laser range finder to the serial port and the camera is connected to an USB port. Nowadays, every computer (esp. laptops) does have these interfaces and therefore the built 3D laser range finder can be used easily on mobile platforms.

The mount and the servo are inexpensive and no special electronic devices are used, so the price of the whole system mainly depends on the used 2D laser range finder.

**Figure 2:** Schloss Birlinghoven.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {schloss.eps}\end{center}\end{figure}$

**Figure 3:** 3D scan of Schloss Birlinghoven, scan time 48 sec with the schmersal scanner over RS232.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {schloss_neu.eps}\end{center}\end{figure}$

Implemented software modules

RealTime Linux module

The servo of the new 3D laser range finder is controlled by a computer running RT-Linux, a real-time operating system which runs LINUX as a task with lowest priority. The servomotor expects a signal every 20 ms, the length of the signal determines the position of the motor (1 ms = leftmost position, 1.5 ms = middle position, 2 ms = rightmost position). This very time critical job has to be done by a real-time operating system, since a latency of about 10 $\mu$ s corresponds to a deviation of $\sim 1^{\circ}$ . Real-time Linux has an average latency of about 5 $\mu$ s (PII-333) and thus the rotation can be realized with an average deviation of $0.5^{\circ}$ .

Online algorithms for line detection

While scanning, different online algorithms for line and surface detection (LENCOMP & HOUGH & LINMER) are applied to the data, thus no extra processing time is needed. Two different kinds of line detection algorithms have been tested 10 (10); 9 (9).

**Figure 4:** Line detection applied to a scan slice
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {scan_l.eps}\end{center}\end{figure}$

The first algorithm (LENCOMP) is a simple straightforward matching algorithm running in $\O(n)$ ( the number of points), with small constants. The algorithm implements a simple length comparison. The data of the laser range finder (points $a_0, a_1, \ldots, a_n$ ) is ordered anticlockwise so that one comparison per point is sufficient. We assume that the points $a_i,\ldots, a_j$ are already on a line. For $a_{j+1}$ we have to check if

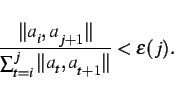$\begin{displaymath} \frac{\Vert a_i, a_{j+1} \Vert}{\sum^j_{t=i}\Vert a_t,a_{t+1} \Vert} < \epsilon(j). \end{displaymath}$

(1)

To obtain better results this algorithm runs on preprocessed data. Data points located close together are joined so the distance from one point to the next point is almost the same (reduction filter). This process minimizes the fluctuations within the data and reduces the points to be processed. Hence this algorithm runs very fast, but the quality of the lines is limited.

The second line detection algorithm implemented is the well known Hough Transformation 12 (12); 11 (11) (see fig. 4). A ( $\rho,\theta$ ) parameterization of the space of lines is used, where $\theta$ is the angle of the normal to the line and $\rho$ the distance along this normal from the line to the origin of the image. A transformation of every point results in a histogram. The maximum of the histogram corresponds to a line and the number of points belonging to this line is maximal.

The iteration of the following three steps returns all line segments.

find maximum = find straight line and calculate the line equation $y=a \cdot x + b$
tag all points belonging to this line
remove these points from the histogram and make line segments

The final step uses the intrinsic order of the data as it comes from the laser range finder. Due to this intrinsic order only one check is necessary to determine whether a point belongs to a line segment. An advantage of the Hough transformation is that it computes the general line equation and all of the belonging line segments in one step which is helpful in further processing steps i.e. 3D surface and 3D object detection.

The Hough-Transformation runs in $\O(d \cdot n$ ), with the distance to the furthest data point. This maximum distance is currently limited to 10 m, so that the transformation can be done in real-time. For indoor environments this limitation is sufficient.

After line detection the transformation of the 2D coordinates into 3D coordinates is done (fig. 5). All following data processing steps operate on the three dimensional data.

**Figure 5:** Composed 3D image from line detection done in 2D planes.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {screen3.eps}\end{center}\end{figure}$

Surface detection

All algorithms described so far run on 2 dimensional data. After line detection is done the data is converted into 3D. Based on the detected lines, the following algorithm LINMER detects surfaces in the 3-dimensional scene.

Scanning a plane surface, the line detection algorithm returns a sequence of lines in successive 2D scans approximate the shape of this surface. Now, the task is to recognize such structures within the 3D data input and to concatenate these independent lines to one single surface. The surface detection algorithm LINMER proceeds the following steps:

The first set of lines - coming from the very first 2D scan - is stored.
Every other line is being checked with the set of stored lines. If a matching line is found, these two lines are transformed into a surface.
If no such matching line exists, the line may be an extension of an already found surface.
In this case, the new line is matching with the top line of a surface. This top line is being replaced by the new line, resulting in an enlarged surface (fig. 6).
Otherwise the line is stored as a stand-alone line in the set mentioned above.

To achieve real time capabilities, the algorithm makes use of the characteristics of the data as it comes from the range finder, i.e. it is the order by the scanned planes. Therefore the lines are sorted throughout the whole scene (with regard to their location within the virtual scene) due to their inherited order. Thus an efficient local search can be realized.

Three criteria have to be fulfilled in order to match lines: First the angle between the two lines has to be smaller than a given value $\delta$ . Second the endpoints of the matching line must be within an $\epsilon$ -area around the corresponding points of the given line (fig. 6). The first constraint is necessary for correct classification of short lines, since they fulfill the distance criterion very easily. To match a line with a surface these two constraints have to hold between the last line of the surface an the new line taken into account. In addition we apply a third constraint that is the line has to lie approximately in the plane given by the surface.

**Figure 6:** Expansion of a surface by a new line
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {surface1.eps}\end{center}\end{figure}$

This step, merely a joining of lines found in former scans, can be done online, too, since no data from future scans is necessary. This means that the robot or a user gets much 3D information about objects in the scenery right during the scan.

Post processing

Offline algorithms (POLYGEN & O-SEG) are used to create a 3D map of the room and to enable a safe navigation of the robot. Despite of the prior algorithms, this step requires information about the whole scene and has to be done after the scan process is finished.

Polygon creation POLYGEN

The surface detection routines creates surfaces consisting of lines. Since the quality of the lines is limited due to noise of the scan data, the result of the surface detection are small surfaces which may even overlap. The task of polygon creation is to merge these surfaces to polygons.
Polygon detection is divided into three steps:

First the LENCOMP algorithm (sec. 3.2) uses the endpoints of all lines of a surface to detect 3D edges. This transforms the line strips into polygons.
After it, each polygon is projected form the 3D coordinate space into a 2D coordinate space of the plane given by the polygon.
Now, the polygons are merged. Since the polygons may overlap this step has to create an overall polygon. The algorithm from Vatti 13 (13) is used as a polygon clipping algorithm.
Each polygon can be a single polygon or a polygon set. Each individual polygon in a polygon set may be convex, concave of self-intersecting. Clipping is defined as interaction of the so called subject polygon and the clipping polygon, hence it is also usable for 2D Boolean operations, e.g. union. If two polygons are approximately within the same plane, these polygons at a time are clipped.
The polygons are striped from bottom to top. Each strip is a horizontal (with respect to the 2D polygon coordinate system) sweep, that is an area between two successive horizontal lines from a set of horizontal lines drawn through all the vertices. During the striping the local maxima and minima are determined, vertices and intersections are classified. From this classification Vattis algorithms computes in our case the overall polygons.
Vattis algorithm runs in linear time in the number of edges of the subject and clipping polygon. The polygon merging algorithm is also used to merge polygons from different scans resulting in a complete surface model of the environment.

As a final step the generated polygons (convex or concave) are transformed into triangle strips only to visualize them in OPENGL.

**Figure 7:** 3D image formed of polygons.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {screen_poly.eps}\end{center}\end{figure}$

Figure 7 shows the result of the polygon merging step applied to the scan shown in figure 5

3D-Object segmentation

3D-Object segmentation (O-SEG) is done by sequentially merging conglomerations of 3D-points, 3D-lines and 3D-surfaces into one 3D-object:

Start with one arbitrary element, i.e. a large 3D-surface. This element is already treated as a ``real'' 3D-object in this state of the algorithm.
Iterate over the previously found elements and check whether there are any elements ``near enough'' to this object. This ``near'' constraint is given by the setup, e.g. one should merge only elements closer than the size of the robot, since the robot can't pass through such objects.
If such an element is found, the object is enlarged until it encloses this element.
Repeat until no more elements fit the given object.

During this process, all elements belonging to the object are marked. The object segmentation algorithm starts again, until no more conglomerations of elements exists, i.e. until no more objects can be found within the scanned scene.

**Figure 8:** Representation of an object
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {object1.eps}\end{center}\end{figure}$

The objects are characterized by bounding boxes (cubes) (fig. 8). A bounding box is given by 3 orthogonal lines, corresponding to the axes of the virtual world coordinate system. In addition, each object is surrounded by a sphere which encloses the whole bounding box. This sphere is used to check very fast whether a single point is near enough to this object to be examined as part of the bounding box.

The O-SEG algorithm first checks if the point is inside the sphere. This can be done by testing the euclidian distance. If the element passes this test, the algorithm determines whether the point is near enough to the actual bounding box. In this case, the lines defining the bounding box have to be re-adjusted to enclose this new point, the sphere likewise.

This procedure can be generalized to handle other kinds of elements as well, since lines are represented by 2 points and surfaces by 2 lines.

Visualization

To visualize the data, a viewer program 2SHOW based on OPENGL was implemented. The task of this program is the projection of the 3D scene to the image plane, i.e. the monitor. A graphical user interface J42SHOW (fig. 9) developed with JAVA enables a simple and easy way to use the scanner application.

**Figure 9:** JAVA user interface
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {java1.eps}\end{center}\end{figure}$

The viewer program can easily be controlled by an extern JAVA panel (fig. 10 & 11). It enables the user to select the element types that are drawn (points, lines, surfaces and objects), to navigate through the 3D scene, to use a simple VCR interface and to extract further information about the scene: clicking on an element returns position, size and - depending on the type of the element - data like number of points within the object, etc.

**Figure 10:** Navigation controlling panel.
$\begin{figure} \begin{center} \epsfsize =110mm \epsfbox {j42show1.eps}\end{center}\end{figure}$

**Figure 11:** Object informations box.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {j42show2.eps}\end{center}\end{figure}$

Results

**Figure:** Application as body scanner a).
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {mybody.ps}\end{center}\end{figure}$

**Figure:** Application as body scanner b).
$\begin{figure} \begin{center} \epsfxsize =100mm \epsfbox {bodytri.eps}\end{center}\end{figure}$

An example (fig. 13 & 14) visualizes the performance of the scanner and the implemented algorithms. It shows the 2nd author taking a video in a corridor and two different views of the scanned scene. The scene was scanned in 12 seconds (schmersal scanner). During the 12 seconds the 115000 data points were reduced to 2596 lines and 977 surfaces. The door on the right side as well as some parts of the walls are detected as flat surfaces. Another interesting application is the use of the 3D laser range finder as a body scanner (fig. 12).

After the scanning process, 180 polygons are created containing only 1144 data points. In addition 60 objects are detected in 2.5 seconds.

Conclusion

This paper has presented a mobile, low-cost, precise and reliable high quality 3D sensor. The 3D laser is built on base of an ordinary 2D range finder and uses only standard computer interfaces. The 3D scanner senses the environment contact-less without the necessity of setting landmarks. The scan resolution for a complete 3D scan of an area of 180 (h) $\times$ 90 (v) degree is up to 194400 points and can be grabbed in 8.1 seconds. The precision is mainly determined by the laser scanner ( $\sim$ 1 cm). Low resolutions e.g. 180 (h) $\times$ 90 (v) degree with 16200 points are grabbed in 1.4 seconds. While scanning, different online algorithms for 3D-line and 3D-surface detection are applied to the data. 3D-Object segmentation and detection are done offline after the scan.

Several products and applications benefits from our 3D laser range finder because it is light, small and very fast:

Autonomous mobile robots. Due to the light weight of the 3D scanner it can be used by mobile robots to survey the environments and to build a precise map. The robots can also detect and avoid complicated obstacles e.g. overhanging obstacles which could not be recognized by 2D distance sensors. Furthermore, all kinds of docking maneuvers even in complicated locations can be done autonomously 14 (14).
Control systems. They uses the 3D information from the scanner to detect and classify objects. Especially machines can be supervised and switch off if humans are in their working area (3D zone defense with a 3d laser range finder).
Facility management systems. Facility management systems require up-to-date informations of the facilities. Especially a complete digital building model which is continuously updated is demanded. The 3D scanner mounted on an autonomous mobile robot can be used to build and update digital building models. Property Management Systems can be used more effectively and more cheaply.

**Figure 13:** Example of a scanned scene
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {video_scene.eps}\end{center}\end{figure}$

**Figure 14:** Two different views on the example scene of figure 13.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {OpenGLPicture_001.eps}\end{center}\end{figure}$

**Figure:** Two different views on the example scene of figure 13.
$\begin{figure} \begin{center} \epsfxsize =110mm \epsfbox {OpenGLPicture_160.eps}\end{center}\end{figure}$

Acknowledgment Special thanks to Stefan Materne and the unknown reviewers for hints and corrections.

Bibliography

Andreas Nuechter Hartmut Surmann, Kai Lingemann and Joachim Hertzberg,: ``A 3d laser range finder for autonomous mobile robots,''
in Proceedings of the of the 32nd ISR (International Symposium on Robotics), Seoul, 2001, pp. 153 - 158.
URL: Sick optic electronic,: ``PLS: Definition der Telegramme zwischen Benutzerschnittstelle und Sensorsystem über RS-422 / RS-232,''
in http://www.sickoptic.com/laser.htm, 2000.
URL: Schmersal EOT,: ``LSS 300: Telegramm zwischen Benutzerschnittstelle und Sensorsystem V.1.14,''
in http:// www.schmersal.de/d/produkte/n2000/laserlss.html, 2000.
S.F. El-Hakim, P. Boulanger, F. Blais, J.A. Beraldin, and G. Roth,: ``A mobile system for indoor 3-d mapping and positioning,''
in Proceedings of the International Symposium on Real-Time Imaging and Dynamic Analysis, Hakodate, Japan, 1998, pp. 331 - 338.
Sebastian Thrun, Dieter Fox, and Wolfram Burgard,: ``A real-time algorithm for mobile robot mapping with applications to multi-robot and 3d mapping,''
in IEEE International Conference on Robotics and Automation, San Francisco, 2000.
Steen Kristensen and Patric Jensfelt,: ``Active global localisation for a mobile robot using multiple hypothesis tracking,''
in Proceedings of the IJCAI'99 Workshop on Reasoning with Uncertainty in Robot Navigation, Stockholm, Sweden, 1999, pp. 13-22.
Axel Walthelm and Amir Madany Momlouk,: ``Multisensoric active spatial exploration and modeling,''
in Dynamische Perzeption: Workshop der GI-Fachgruppe 1.0.4 Bildverstehen, Ulm. 2000, pp. 141-146, AKA Akad. Verl.-Ges., Berlin.
URL: amtec,: ``amtec product homepage,''
in http://www.powercube.de/index_products.html, 1999.
Michael Pauly, Hartmut Surmann, Marion Finke, and Nang Liang,: ``Real-time object detection for autonomous robots,''
Informatik Aktuell. Autonome Mobile Systeme, 14. Fachgespräch, Springer-Verlag, pp. 57-64, 1998.
J.-S. Gutmann,: Robuste Navigation autonomer mobiler Systeme (in German), Doctoral Thesis,
Akademische Verlagsgesellschaft Aka, Berlin, 2000.
P. V. C. Hough,: ``Methods and means for recognising complex patterns,''
in U.S. Patent 3 069 654, Dec 1962.
R. A. McLaughlin and M. D. Alder,: ``The hough transform versus the upwrite,''
IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 20, no. 4, pp. 396-400, 1998.
Bala R. Vatti,: ``A generic solution to polygon clipping,''
Communications of the ACM, , no. 7, pp. 56-63, 07/1992.
Günther Schmidt Joachim Horn,: ``Continuous localization of a mobile robot based on 3d-laser-range-data, predicted sensor images and dead-reckoning,''
Robotics and Autonomous Systems, vol. 14, pp. 99 - 118, 1995.

... surfaces

The 3D scene can be seen at http://www.ais.fraunhofer.de/ARC/3D/

Hartmut Surmann
2001-10-17