


Next: 3D Object Detection
Up: The Autonomous Mobile Robot
Previous: Basic 3D Scanner Software
To create a correct and consistent representation of the environment,
the acquired 3D scans have to be merged in one coordinate
system. This process is called registration. Due to the robot's
sensors, the self-localization is usually erroneous and
imprecise, so the geometric structure of overlapping 3D scans has
to be considered for registration. The odometry-based robot pose
serves as a first estimate and is corrected and updated by the
registration process. We use the well-known Iterative Closest
Points (ICP) algorithm [2] to compute the
transformation, consisting of a rotation
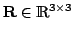 and a translation
and a translation
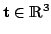 . The ICP algorithm
computes this transformation in an iterative fashion. In each iteration
the algorithm selects the closest points as correspondences
and computes the transformation (
. The ICP algorithm
computes this transformation in an iterative fashion. In each iteration
the algorithm selects the closest points as correspondences
and computes the transformation (
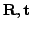 ) for minimizing
) for minimizing
where 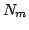 and
and 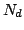 are the number of points in the model set
are the number of points in the model set
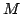 , i.e., first 3D scan, or data set
, i.e., first 3D scan, or data set 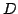 , second 3D scan,
respectively, and
, second 3D scan,
respectively, and 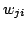 are the weights for a point match. The
weights are assigned as follows:
are the weights for a point match. The
weights are assigned as follows:
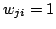 , if
, if
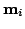 is the
closest point to
is the
closest point to
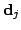 within a close limit,
within a close limit,
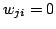 otherwise. It is shown in [2] that the iteration
terminates in a minimum.
The assumption is that in the last iteration
the point correspondences are correct. In each iteration
the transformation is computed in a fast closed-form manner by
the quaternion-based method of Horn [8]. In addition,
point reduction and
otherwise. It is shown in [2] that the iteration
terminates in a minimum.
The assumption is that in the last iteration
the point correspondences are correct. In each iteration
the transformation is computed in a fast closed-form manner by
the quaternion-based method of Horn [8]. In addition,
point reduction and 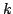 D.trees speed up the computation of the
point pairs, such that only the time required for scan matching is
reduced to roughly one second
[17]. Figure 3 shows three iteration steps
for 3D scan alignment.
D.trees speed up the computation of the
point pairs, such that only the time required for scan matching is
reduced to roughly one second
[17]. Figure 3 shows three iteration steps
for 3D scan alignment.
Figure 3:
Three iteration steps of scan alignment process for the
two 3D scans presented in Figure 1 (bottom, middle,
right).
|
|



Next: 3D Object Detection
Up: The Autonomous Mobile Robot
Previous: Basic 3D Scanner Software
root
2004-06-02
![]() and a translation
and a translation
![]() . The ICP algorithm
computes this transformation in an iterative fashion. In each iteration
the algorithm selects the closest points as correspondences
and computes the transformation (
. The ICP algorithm
computes this transformation in an iterative fashion. In each iteration
the algorithm selects the closest points as correspondences
and computes the transformation (
![]() ) for minimizing
) for minimizing
![\includegraphics[width=38mm,height=34mm]{merge3}](img42.png)
![\includegraphics[width=38mm,height=34mm]{merge2}](img43.png)
![\includegraphics[width=38mm,height=34mm]{merge1}](img44.png)