


Next: State of the Art
Up: Background
Previous: Background
The ICP Algorithm was developed by Besl and McKay
[5] and is usually used to register two given point
sets in a common coordinate system. The algorithm calculates
iteratively the registration. In each iteration step, the
algorithm selects the closest points as correspondences and
calculates the transformation, i.e., rotation and translation
(
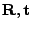 ), for minimizing the equation
), for minimizing the equation
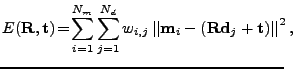 |
|
|
(1) |
where 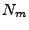 and
and 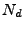 , are the number of points in the model set
, are the number of points in the model set 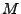 and data set
and data set 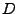 , respectively, and
, respectively, and 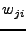 are the weights for a point
match. The weights are assigned as follows:
are the weights for a point
match. The weights are assigned as follows:
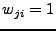 , if
, if
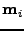 is the closest point to
is the closest point to
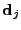 ,
,
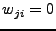 otherwise. Eq. (1) can be reduced to
otherwise. Eq. (1) can be reduced to
with
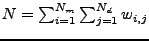 , since the
correspondence matrix can be represented by a vector
, since the
correspondence matrix can be represented by a vector
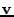 containing
the point pairs, i.e.,
containing
the point pairs, i.e.,
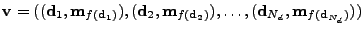 , with
, with
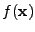 the search function returning the closest point. The
assumption is that in the last iteration step the point
correspondences, thus the vector of point pairs, are correct.
the search function returning the closest point. The
assumption is that in the last iteration step the point
correspondences, thus the vector of point pairs, are correct.
In each ICP iteration, the transformation can be calculated by any of
these four methods: A SVD based method of Arun et
al. [1], a quaternion method of Horn [12], an
algorithm using orthonormal matrices of Horn et al. [13]
and a calculation based on dual quaternions of Walker et
al. [24]. These algorithms show similar performance and
stability concerning noisy data [15].
Besl and McKay show that the iteration terminates in a minimum
[5]. Note: Normally, implementations of ICP would use a
maximal distance for closest points to handle partially overlapping
point sets. In this case the proof in [5] does no longer
hold, since the number of points as well as the value of
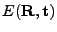 might increase after applying a transformation.
might increase after applying a transformation.



Next: State of the Art
Up: Background
Previous: Background
root
2007-05-31
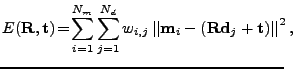
![]() might increase after applying a transformation.
might increase after applying a transformation.