

Next: Learning Classification Functions
Up: Object Classification
Previous: Object Classification
There are many motivations for using features
rather than pixels directly. For mobile robots, a critical
motivation is that feature based systems operate much faster than
pixel based systems [#!Viola_2001!#]. The features used here
have the same structure as the Haar basis functions, i.e., step
functions introduced by Alfred Haar to define wavelets
[#!Haar_1910!#]. They are also used in
[#!Lienhart_2003_1!#,#!Lienhart_2002!#,#!Papageorgio_1998!#,#!Viola_2001!#].
Figure 2 (left) shows the six basis features, i.e.,
edge, line, and center surround features. The base resolution of
the object detector is 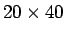 pixels, thus the set of
possible features in this area is very large (361760 features).
In contrast to the Haar basis function, the set of rectangle
features is not minimal. A single feature is effectively computed
on input images using integral images [#!Viola_2001!#], also
known as summed area tables [#!Lienhart_2003_1!#,#!Lienhart_2002!#]. An integral image
pixels, thus the set of
possible features in this area is very large (361760 features).
In contrast to the Haar basis function, the set of rectangle
features is not minimal. A single feature is effectively computed
on input images using integral images [#!Viola_2001!#], also
known as summed area tables [#!Lienhart_2003_1!#,#!Lienhart_2002!#]. An integral image 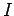 is an intermediate
representation for the image and contains the sum of gray scale
pixel values of image
is an intermediate
representation for the image and contains the sum of gray scale
pixel values of image 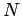 with height
with height 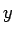 and width
and width 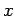 , i.e.,
, i.e.,
The integral image is computed recursively, by the
formulas:
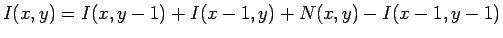 with
with
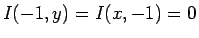 , therefore requiring only
one scan over the input data. This intermediate representation
, therefore requiring only
one scan over the input data. This intermediate representation
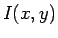 allows the computation of a rectangle feature value at
allows the computation of a rectangle feature value at
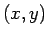 with height and width
with height and width 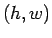 using four references (see
Figure 2 (right)):
using four references (see
Figure 2 (right)):
Since the features are a composition of
rectangles, they are computed with several lookups and
subtractions weighted with the area of the black and white
rectangles. To detect a feature, a threshold is required. This
threshold is automatically determined during a fitting process,
such that a minimum number of examples are misclassified. The
examples are given in a set of images that are classified as
positive or negative samples. The set is also used in the
learning phase that is briefly described next.


Next: Learning Classification Functions
Up: Object Classification
Previous: Object Classification
root
2004-03-04
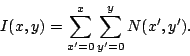
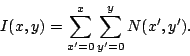
![]() with
with
![]() , therefore requiring only
one scan over the input data. This intermediate representation
, therefore requiring only
one scan over the input data. This intermediate representation
![]() allows the computation of a rectangle feature value at
allows the computation of a rectangle feature value at
![]() with height and width
with height and width ![]() using four references (see
Figure 2 (right)):
using four references (see
Figure 2 (right)):