

Next: Computing Globally Consistent Scenes
Up: ICP-based 6D SLAM
Previous: ICP-based 6D SLAM
Calculating Heuristic Initial Estimations for ICP Scan Matching
To match two 3D scans with the ICP algorithm it is necessary to
have a sufficient starting guess for the second scan pose. In
earlier work we used odometry [23] or the planar HAYAI
scan matching algorithm [16]. However, the latter
cannot be used in arbitrary environments, e.g., the one presented
in Fig. 1 (bad asphalt, lawn,
woodland, etc.). Since the motion models change with different
grounds, odometry alone cannot be used. Here the robot pose is
the 6-vector
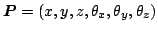 or, equivalently the tuple containing the rotation
matrix and translation vector, written as 4
or, equivalently the tuple containing the rotation
matrix and translation vector, written as 4 4 OpenGL-style
matrix
4 OpenGL-style
matrix  [8].
[8].![[*]](footnote.png) The
following heuristic computes a sufficiently good initial
estimation. It is based on two ideas. First, the transformation
found in the previous registration is applied to the pose
estimation - this implements the assumption that the error model
of the pose estimation is locally stable. Second, a pose update
is calculated by matching octree representations of the scan
point sets rather than the point sets themselves - this is done
to speed up calculation:
The
following heuristic computes a sufficiently good initial
estimation. It is based on two ideas. First, the transformation
found in the previous registration is applied to the pose
estimation - this implements the assumption that the error model
of the pose estimation is locally stable. Second, a pose update
is calculated by matching octree representations of the scan
point sets rather than the point sets themselves - this is done
to speed up calculation:
- Extrapolate the odometry readings to all six degrees of freedom
using previous registration matrices. The change of the robot
pose
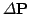 given the odometry information
given the odometry information
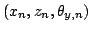 ,
,
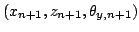 and the registration matrix
and the registration matrix
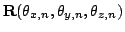 is calculated by solving:
is calculated by solving:
Therefore, calculating
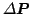 requires a matrix
inversion. Finally, the 6D pose
requires a matrix
inversion. Finally, the 6D pose
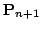 is calculated by
is calculated by
using the poses' matrix representations.
- Set
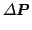 best to the 6-vector
best to the 6-vector
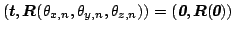 .
.
- Generate an octree
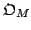 for the
for the 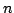 th 3D scan (model set
th 3D scan (model set 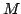 ).
).
- Generate an octree
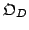 for the
for the 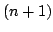 th 3D scan (data set
th 3D scan (data set 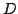 ).
).
- For search depth
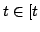 Start
Start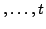 End
End![$ ]$](img67.png) in the octrees estimate a transformation
in the octrees estimate a transformation
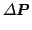 best
best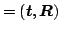 as follows:
as follows:
- Calculate a maximal displacement and rotation
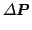 max depending on the search depth
max depending on the search depth 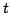 and currently best
transformation
and currently best
transformation
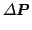 best.
best.
- For all discrete 6-tuples
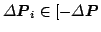 max
max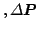 max
max![$ ]$](img67.png) in the domain
in the domain
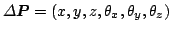 displace
displace
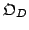 by
by
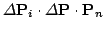 . Evaluate the matching of the two octrees by counting the
number of overlapping cubes and save the best
transformation as
. Evaluate the matching of the two octrees by counting the
number of overlapping cubes and save the best
transformation as
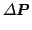 best.
best.
- Update the scan pose using matrix multiplication, i.e.,
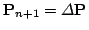 best best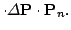 |
|
|
|
Figure 2:
Left: Two 3D point clouds. Middle: Octree corresponding
to the black point cloud. Right: Octree based on the blue
points.
|
|
Note: Step 5b requires 6 nested loops, but the
computational requirements are bounded by the coarse-to-fine
strategy inherited from the octree processing. The size of the
octree cubes decreases exponentially with increasing 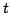 . We
start the algorithm with a cube size of 75 cm
. We
start the algorithm with a cube size of 75 cm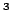 and stop when
the cube size falls below 10 cm
and stop when
the cube size falls below 10 cm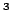 . Fig. 2 shows
two 3D scans and the corresponding octrees. Furthermore, note
that the heuristic works best outdoors. Due to the diversity of
the environment the match of octree cubes will show a
significant maximum, while indoor environments with their many
geometry symmetries and similarities, e.g., in a corridor, are
in danger of producing many plausible matches.
. Fig. 2 shows
two 3D scans and the corresponding octrees. Furthermore, note
that the heuristic works best outdoors. Due to the diversity of
the environment the match of octree cubes will show a
significant maximum, while indoor environments with their many
geometry symmetries and similarities, e.g., in a corridor, are
in danger of producing many plausible matches.
After an initial starting guess is found, the range image
registration from section 2 proceeds and the 3D scans are
precisely matched.


Next: Computing Globally Consistent Scenes
Up: ICP-based 6D SLAM
Previous: ICP-based 6D SLAM
root
2005-06-17
![[*]](footnote.png) The
following heuristic computes a sufficiently good initial
estimation. It is based on two ideas. First, the transformation
found in the previous registration is applied to the pose
estimation - this implements the assumption that the error model
of the pose estimation is locally stable. Second, a pose update
is calculated by matching octree representations of the scan
point sets rather than the point sets themselves - this is done
to speed up calculation:
The
following heuristic computes a sufficiently good initial
estimation. It is based on two ideas. First, the transformation
found in the previous registration is applied to the pose
estimation - this implements the assumption that the error model
of the pose estimation is locally stable. Second, a pose update
is calculated by matching octree representations of the scan
point sets rather than the point sets themselves - this is done
to speed up calculation:
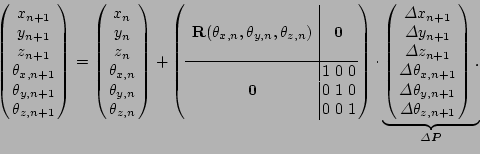
![\includegraphics[width=0.325\linewidth]{octree1_2}](img76.png)
![\includegraphics[width=0.325\linewidth]{octree1}](img77.png)
![\includegraphics[width=0.325\linewidth]{octree2}](img78.png)