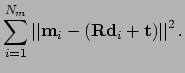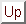

Next: Mesh Generation
Up: Automatic Reconstruction of Colored
Previous: The Camera System
Camera Calibration
The camera is modeled by the usual pinhole approach. A camera
projects a 3D point
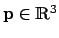 to the 2D image, resulting
in
to the 2D image, resulting
in
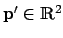 . The relationship between a 3D point
. The relationship between a 3D point 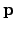 and its image projection
and its image projection 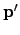 is given by
is given by
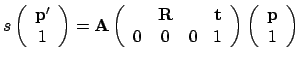 with with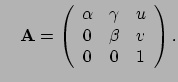 |
|
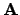 is the camera matrix, i.e., internal camera parameters,
with the principal point with the coordinates
is the camera matrix, i.e., internal camera parameters,
with the principal point with the coordinates 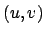 .
. 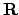 and
and 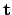 specify the external camera parameters, i.e., the
orthonormal
specify the external camera parameters, i.e., the
orthonormal
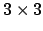 rotation matrix and translation vector
of the camera in the world coordinate system. In addition to
these equations, we consider the distortion, resulting in 4
additional parameters to estimate [#!zhang_2000!#].
rotation matrix and translation vector
of the camera in the world coordinate system. In addition to
these equations, we consider the distortion, resulting in 4
additional parameters to estimate [#!zhang_2000!#].
Figure:
Top: Chessboard plane for calibration. Bottom:
Chessboard detection in a 3D laser range scan.
51mm
![\includegraphics[width=51mm,height=51mm]{zhangSchachbrett}](img22.png)
![\includegraphics[width=51mm,height=51mm]{chessMatch}](img23.png) |
Camera calibration uses a new technique based on Zhang's
method. We give a brief sketch here, details can be found in
[#!zhang_2000!#]. The key idea behind Zhang's approach is to
estimate the intrinsic, extrinsic and distortion camera
parameters by a set of corresponding point. These 3D-to-2D point
correspondences are first used to derive an analytical solution,
i.e., the general
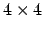 homography matrix
homography matrix  is
estimated:
is
estimated:
The estimation is done by solving an over specified system of linear
equations. Since the points of 3D-to-2D point correspondences have
usually small errors and only a few points are used to solve the
equations for  , this first estimation needs to be optimized. A
nonlinear optimization technique, i.e, the Levenberg-Marquardt
algorithm based on the maximum likelihood criterion is used to
optimize the error term:
, this first estimation needs to be optimized. A
nonlinear optimization technique, i.e, the Levenberg-Marquardt
algorithm based on the maximum likelihood criterion is used to
optimize the error term:
Hereby
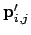 are the points
are the points
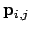 projected by
projected by 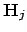 , and
, and
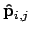 are the given corresponding points;
are the given corresponding points; 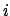 is the point index and
is the point index and 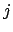 is the image index. After the calculation
of
is the image index. After the calculation
of  , the camera matrix
, the camera matrix 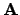 , the rotation matrix
, the rotation matrix 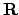 and
the translation
and
the translation 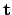 are calculated from
are calculated from  . Again, an over
specified system of linear equation is solved, followed by a nonlinear
optimization of
. Again, an over
specified system of linear equation is solved, followed by a nonlinear
optimization of
Finally the term for optimization is set to
where 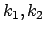 are parameters for the radial distortion, and
are parameters for the radial distortion, and
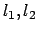 the ones for tangential distortion. The minimum is
found by the Levenberg-Marquardt algorithm that combines gradient
descent and Gauss-Newton approaches for function minimization
[#!Fitzgibbon_2001!#,#!NumericalRecipes!#]. An important concept of
the Levenberg-Marquardt algorithm is the vector of residuals,
i.e.,
the ones for tangential distortion. The minimum is
found by the Levenberg-Marquardt algorithm that combines gradient
descent and Gauss-Newton approaches for function minimization
[#!Fitzgibbon_2001!#,#!NumericalRecipes!#]. An important concept of
the Levenberg-Marquardt algorithm is the vector of residuals,
i.e.,
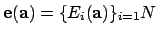 , so that
, so that
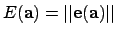 is one of the error terms above. The
goal at each iteration is to choose an update
is one of the error terms above. The
goal at each iteration is to choose an update 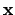 to the
current estimate
to the
current estimate 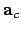 , such that setting
, such that setting
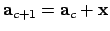 reduces the error
reduces the error 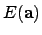 . A Taylor approximation of
. A Taylor approximation of
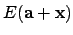 results in
results in
Expressing this approximations in terms of 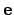 yields [#!Fitzgibbon_2001!#]:
yields [#!Fitzgibbon_2001!#]:
By neglecting the therm
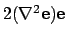 the Gauss-Newton
approximation is derived, i.e.,
the Gauss-Newton
approximation is derived, i.e.,
with 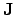 the Jacobian matrix
the Jacobian matrix 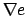 , i.e.,
, i.e.,
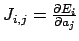 . The task at each iteration is
to determine a step
. The task at each iteration is
to determine a step 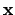 that will minimize
that will minimize
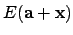 . Using the approximation of
. Using the approximation of 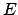 differentiating with respect
to
differentiating with respect
to 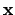 equating with zero, yields
equating with zero, yields
Solving this equation for 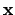 yields the new Gauss-Newton
update
yields the new Gauss-Newton
update
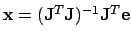 . In contrast, the
update with an accelerated gradient descent is given by
. In contrast, the
update with an accelerated gradient descent is given by
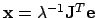 with
with 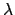 denoting the increment
between two gradient descent steps. In every iteration this new
update is calculated by a combination, i.e., by
denoting the increment
between two gradient descent steps. In every iteration this new
update is calculated by a combination, i.e., by
For the above camera calibration algorithm the 3D-to-2D point
correspondences are essential. Calibration is done with a chess
board. From the image the board pattern corners are extracted
automatically (Fig. 3 top). The corresponding 3D
points are automatically extracted based on the corners of a quad
in 3D (Fig. 3 bottom). The calibration algorithm
extracts the 3D quad from the scanned point cloud with a modified
ICP (Iterative Closest Points) algorithm
[#!Besl_1992!#,#!IAV!#]. Given a set of 3D scan points 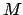 , a quad
is matched. The algorithm computes the rotation
, a quad
is matched. The algorithm computes the rotation 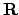 and the
translation
and the
translation 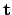 , such that the distances the scan points
, such that the distances the scan points
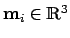 and their projection to the quad
and their projection to the quad
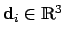 is minimized, i.e.,
is minimized, i.e.,
The ICP algorithm accomplishes the minimization iteratively. It
computes first the projections and then minimizes the above error
term in a closed form fashion [#!Besl_1992!#,#!IAV!#]. The
closed form solution is based on the representation of a rotation
as a quaternion as proposed by Horn [#!Horn_1987!#].


Next: Mesh Generation
Up: Automatic Reconstruction of Colored
Previous: The Camera System
root
2004-04-16
![]() to the 2D image, resulting
in
to the 2D image, resulting
in
![]() . The relationship between a 3D point
. The relationship between a 3D point ![]() and its image projection
and its image projection ![]() is given by
is given by
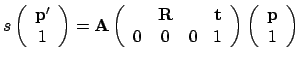 with
with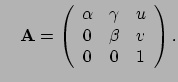
![\includegraphics[width=51mm,height=51mm]{zhangSchachbrett}](img22.png)
![\includegraphics[width=51mm,height=51mm]{chessMatch}](img23.png)
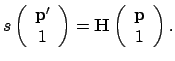
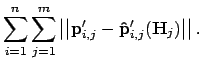
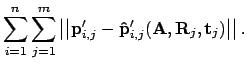
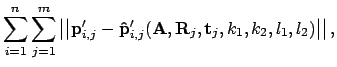
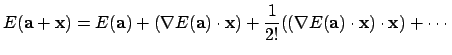
![]() , a quad
is matched. The algorithm computes the rotation
, a quad
is matched. The algorithm computes the rotation ![]() and the
translation
and the
translation ![]() , such that the distances the scan points
, such that the distances the scan points
![]() and their projection to the quad
and their projection to the quad
![]() is minimized, i.e.,
is minimized, i.e.,