


Next: Item 2: Heuristic Initial
Up: The Context: Outdoor SPLAM
Previous: The Context: Outdoor SPLAM
We first extrapolate the odometry readings to all six degrees of
freedom using previous registration matrices. The robot pose is
the 6-vector
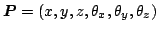 or, equivalently the tuple containing the rotation
matrix and translation vector, written as 4
or, equivalently the tuple containing the rotation
matrix and translation vector, written as 4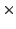 4 OpenGL-style
matrix
4 OpenGL-style
matrix 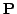 [7].1The change of the robot pose
[7].1The change of the robot pose
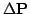 given the odometry
information
given the odometry
information
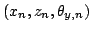 ,
,
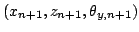 and the registration matrix
and the registration matrix
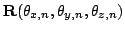 is
calculated by solving:
is
calculated by solving:
Therefore, calculating
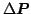 requires a matrix
inversion. Finally, the 6D pose
requires a matrix
inversion. Finally, the 6D pose
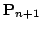 is calculated by
is calculated by
using the poses' matrix representations.
root
2006-03-16
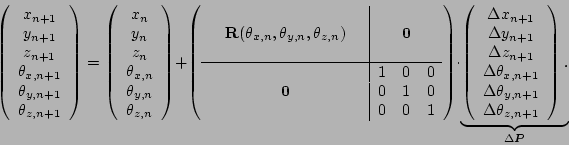
![]() requires a matrix
inversion. Finally, the 6D pose
requires a matrix
inversion. Finally, the 6D pose
![]() is calculated by
is calculated by