


Next: Item 3: ICP for
Up: The Context: Outdoor SPLAM
Previous: Item 1: Odometry Extrapolation.
Initial estimations for ICP scan matching are computed with an
octree based heuristic. The algorithm sets initially
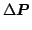 best to the 6-vector
best to the 6-vector
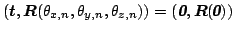 . Then, an octree
. Then, an octree  for the
for the 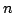 th 3D scan
(model set
th 3D scan
(model set 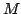 ) and an octree
) and an octree 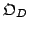 for the
for the 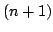 th 3D scan
(data set
th 3D scan
(data set 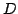 ) is generated (cf. Fig. 2). The
estimation is done for search depth
) is generated (cf. Fig. 2). The
estimation is done for search depth
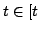 Start
Start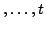 End
End![$ ]$](img30.png) in the octrees. Hereby a a
transformation
in the octrees. Hereby a a
transformation
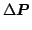 best
best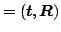 is
computed as follows:
is
computed as follows:
- Calculate a maximal displacement and rotation
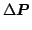 max depending on the search depth
max depending on the search depth 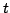 and currently best
transformation
and currently best
transformation
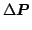 best.
best.
- For all discrete 6-tuples
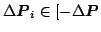 max
max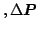 max
max![$ ]$](img30.png) in the domain
in the domain
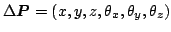 displace
displace
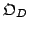 by
by
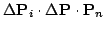 . Evaluate the matching of the two octrees by counting the
number of overlapping cubes and save the best
transformation as
. Evaluate the matching of the two octrees by counting the
number of overlapping cubes and save the best
transformation as
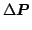 best.
best.
Finally, the scan pose is updated using matrix multiplication, i.e.,
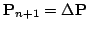 best best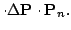 |
|
|
|
Note: Step 2 requires 6 nested loops, but the
computational requirements are bounded by the coarse-to-fine
strategy inherited from the octree processing. The size of the
octree cubes decreases exponentially with increasing 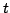 . We
start the algorithm with a cube size of 75 cm
. We
start the algorithm with a cube size of 75 cm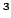 and stop when
the cube size falls below 10 cm
and stop when
the cube size falls below 10 cm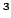 . Fig. 2 shows
two 3D scans and the corresponding octrees. Furthermore, note
that this heuristic works best outdoors. Due to the diversity of
the environment the match of octree cubes will show a
significant maximum, while indoor environments with their many
geometry symmetries and similarities, e.g., in a corridor, are
in danger of producing many plausible matches.
. Fig. 2 shows
two 3D scans and the corresponding octrees. Furthermore, note
that this heuristic works best outdoors. Due to the diversity of
the environment the match of octree cubes will show a
significant maximum, while indoor environments with their many
geometry symmetries and similarities, e.g., in a corridor, are
in danger of producing many plausible matches.
Figure 2:
Left: Two 3D point clouds. Middle: Octree corresponding
to the black point cloud. Right: Octree based on the blue
points.
|
|



Next: Item 3: ICP for
Up: The Context: Outdoor SPLAM
Previous: Item 1: Odometry Extrapolation.
root
2006-03-16
![]() . We
start the algorithm with a cube size of 75 cm
. We
start the algorithm with a cube size of 75 cm![]() and stop when
the cube size falls below 10 cm
and stop when
the cube size falls below 10 cm![]() . Fig. 2 shows
two 3D scans and the corresponding octrees. Furthermore, note
that this heuristic works best outdoors. Due to the diversity of
the environment the match of octree cubes will show a
significant maximum, while indoor environments with their many
geometry symmetries and similarities, e.g., in a corridor, are
in danger of producing many plausible matches.
. Fig. 2 shows
two 3D scans and the corresponding octrees. Furthermore, note
that this heuristic works best outdoors. Due to the diversity of
the environment the match of octree cubes will show a
significant maximum, while indoor environments with their many
geometry symmetries and similarities, e.g., in a corridor, are
in danger of producing many plausible matches.
![\includegraphics[width=0.325\linewidth]{octree1_2}](img40.png)
![\includegraphics[width=0.325\linewidth]{octree1}](img41.png)
![\includegraphics[width=0.325\linewidth]{octree2}](img42.png)