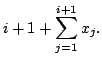First, we introduce some notation that will be used throughout this section.
Let us assume that the corner that hides the object
is at distance ![]() from the start.
Let
from the start.
Let ![]() denote the distance the robot travels in the
denote the distance the robot travels in the
![]() th step, i.e., on its way from position
th step, i.e., on its way from position ![]() to position
to position ![]() ,
from which the
,
from which the ![]() th scan will be taken.
If the object was hidden infinitesimally behind position
th scan will be taken.
If the object was hidden infinitesimally behind position ![]() ,
the optimal solution would go perpendicularly to the line
,
the optimal solution would go perpendicularly to the line ![]() that runs
from the corner through position
that runs
from the corner through position ![]() , and then take one scan from there.
Let
, and then take one scan from there.
Let ![]() denote the length of this line segment and observe that it meets
denote the length of this line segment and observe that it meets ![]() at a point that lies on the semi-circle spanned by the start
and the corner.
Then the optimum cost to detect the object would be
at a point that lies on the semi-circle spanned by the start
and the corner.
Then the optimum cost to detect the object would be ![]() , whereas the robot
would only see the object at position
, whereas the robot
would only see the object at position ![]() , having accumulated a cost of
, having accumulated a cost of