Globally Optimal Strategies

The above recursion can be used for proving a lower bound.

Assume the claim was false, and there was a $c$-competitive strategy for $c=2-\delta$. We show that $x_i \leq (1-\delta)^i$ holds, making it impossible for the robot to get further than a distance of $1/\delta$ away from the start, a contradiction. Clearly, we have $x_1=1-\delta$ for step 1. Moreover,

$$d_i \leq \sum_{j=1}^i x_j$$

holds, because $d_i$ is the shortest path from the start to line $L_i$, whereas the sum denotes the length of the robot's path. Plugging this into our recursion yields

$$x_{i+1} \leq (1 - \delta) (1+\sum_{j=1}^i x_j) -i.$$

By induction, we have $x_j \leq (1-\delta)^j$, hence

$$x_{i+1} \leq (1 - \delta)\frac{1-(1-\delta)^{i+1}}{\delta} -i \leq (1-\delta)\frac{1-(1-(1+i)\delta)}{\delta} -i$$

$$= 1-(1+i)\delta \leq (1-\delta)^{i+1},$$

using the Bernoulli inequality $1-(1+i)\delta \leq (1-\delta)^{i+1}$ twice. $\qedsymbol$

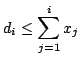
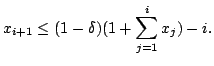
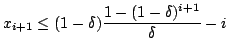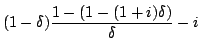Instead of increasing the distance $d$ we could as well consider a situation where start and corner are a distance 1 apart, but the scan cost is only $1/d$. Now Theorem 1 shows a remarkable discontinuity: Even for a scan cost arbitrarily small, a lower bound of 2 cannot be beaten, whereas for zero scan cost, a factor of $1.212\dots$ can be obtained [9].

On the positive side, for $n$ intermediate scan points, Equation (1) provides $n$ optimality conditions. As there are $2n$ degrees of freedom (the coordinates of intermediate scan points), we get an underdetermined nonlinear optimization problem for any given distance $d$, provided that we know the number of scan points. For $d=1$, this can be used to derive an optimal competitive factor of 1.808201..., achieved with one intermediate scan point. For larger $d$ (and hence, larger $n$) one could derive additional geometric optimality conditions and use them in combination with more complex numerical methods. However, this approach appears impractical for real applications, for reasons stated above. As we will see in the following, there is a better approach.

ARRAY(0x93985d0)