A Simple Heuristic Strategy

Now we describe a simple strategy for the searching problem that uses trajectories inscribed into a circle. This reduces the degrees of freedom to the point where evaluation is fast and easy. What is more, it works very well in realistic settings, and it is asymptotically optimal for decreasing cost of scanning, or growing size of the environment.

The robot simply follows a polygonal path inscribed into the semi-circle of diameter $d$, spanned by start and corner. It remains to determine those points where it stops for scanning its environment. This is done by applying the optimality condition derived in Section 3.1. In step $j$, the robot moves along a chord of length $x_j$. From the corner, this chord is visible under an angle of $\varphi_j= \arcsin(x_j/d)$. The chord connecting the start to position $i$ is of length

$$d_i = d \sin( \sum_{j=1}^i \varphi_j),$$

so that the recursion (1) obtained in Section 3.1 turns into

$$x_{i+1} = c\left(1+d \sin\left(\sum_{j=1}^{i}\arcsin\left(\frac{x_j}{d}\right)\right)\right) -(i+1)-\sum_{j=1}^{i}x_j.$$

Given any $c>1$, we can tentatively compute steps of length $x_i$ by this formula, starting with $x_1 = c-1$. If the resulting sequence reaches the corner, the ratio of $c$ can indeed be achieved. If it collapses prematurely (by returning negative values) $c$ was too small. (For example, $c=2.001525...$ is optimal for $d=40$; see Figure 3.3 for an illustration of upper and lower bounds on this value.)

Figure 5: An example for $d=40$, with starting point on the right, corner on the left of the semi-circles: (Left) For $c=2.0016$, the circle sequence reaches the corner, showing that the chosen $c$ can be achieved. (Right) For $c=2.0015$, the sequence collapses before reaching the corner, showing that the chosen $c$ cannot be achieved. The actual optimum is about 2.001525...

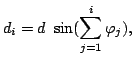
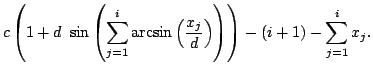By performing a binary search, the optimal ratio and the necessary step lengths can be computed extremely fast. Moreover, an analysis of the optimal ratio as a function of $d$ shows that a maximum is reached for $d=4.400875...$ which is precisely at the threshold between three and four necessary scans, with a competitive ratio of 2.168544. (See Table 1 for an overview of the critical values for which the number of scans increases, and Figure 7 for the achievable ratios as a function of the distance.) This is still within about 2% of the global optimum, which appears to be at about 2.12 (see Figure 6.) Moreover, numerical evidence shows that the ratio approaches 2 quite rapidly as $d$ tends to infinity. This is all the more surprising, as the resulting initial step length converges to 1, while a constant step length of 1 yields a competitive ratio of $\pi$. In the following Section 3.4 we give a mathematical proof of this observation.

Table 1: Threshold values for small numbers of scans, rounded to six digits.

Number	Maximal	$c$ at
of scans	$d$	upper bound
0	0.618034	1.618034
1	1.530414	2.040287
2	2.799395	2.155363
3	4.400876	2.168544
4	6.316892	2.147994
5	8.514200	2.118498

Figure 6: A solution for $d=4.4$ that achieves competitive ratio 2.12: The starting position is at $A$, the corner at $B$.

Figure 7: The competitive ratio as a function of $d$: (Left) for small values of $d$. (Right) for larger values of $d$. Note the cusps at threshold values, the sharp peak at (4.4,2.17), and the clear asymptotic behavior. The first step length, $x_1$, is given by $c-1$.