As we have seen in Theorem 1, there is a
lower bound of 2 on the competitive ratio for all strategies and large ![]() .
In the following we will show that for large
.
In the following we will show that for large ![]() , there is a matching
upper bound on our circle strategy presented in Section 3.3,
proving it to be asymptotically optimal. For limited physical distances,
it shows that even for arbitrarily small scan times, there is a
relatively simple strategy that achieves the optimal ratio of 2.
, there is a matching
upper bound on our circle strategy presented in Section 3.3,
proving it to be asymptotically optimal. For limited physical distances,
it shows that even for arbitrarily small scan times, there is a
relatively simple strategy that achieves the optimal ratio of 2.
Our proof of the upper bound proceeds as follows. Let us assume that we are given
some fixed
 .
We then proceed to show that
for
.
We then proceed to show that
for
![]() , the recursion presented in Section 3.3
does not collapse before the corner is reached, if the diameter
, the recursion presented in Section 3.3
does not collapse before the corner is reached, if the diameter ![]() of the
semi-circle is large enough.
of the
semi-circle is large enough.
In proving the lower bound
stated in Theorem 1, we have used the obvious fact that
the length ![]() of the optimal path cannot exceed the length of the robot's
path. Now we are turning this argument around: The robot's path to position
of the optimal path cannot exceed the length of the robot's
path. Now we are turning this argument around: The robot's path to position ![]() does not exceed the length of the circular arc leading from the start to
position
does not exceed the length of the circular arc leading from the start to
position ![]() . As this arc is not much longer than
. As this arc is not much longer than
![]() , the length of the chord
from the start to
, the length of the chord
from the start to ![]() , if the diameter
, if the diameter ![]() of the circle is large enough.
More precisely, we use the following.
of the circle is large enough.
More precisely, we use the following.
Claim (i) can be shown by the same technique as in the proof of
Theorem 1. In order to prove claim (ii), let ![]() and
and ![]() denote the maximum lengths of an arc and its chord in a circle of
diameter
denote the maximum lengths of an arc and its chord in a circle of
diameter ![]() satisfying
satisfying
![]() . Let
. Let ![]() denote
the angle of the arc, as seen
from the center, so that
denote
the angle of the arc, as seen
from the center, so that ![]() and
and
![]() hold. The maximum arc
satisfying the condition is of length
hold. The maximum arc
satisfying the condition is of length
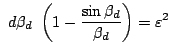 where
where ![]() is the
solution of the equation
is the
solution of the equation
![]() . In the
equivalent expression
. In the
equivalent expression
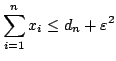
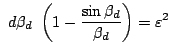 must be unbounded.
must be unbounded.
These facts will now be used in providing a lower bound for the first steps
along the semi-circle, aiming for a competitive
ratio of
![]() .
.
Using Lemma 1 we can choose ![]() large enough that
large enough that
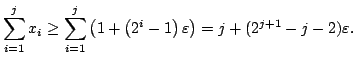 ,
and let
,
and let 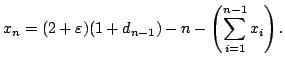 be the
be the
As ![]() ,
we have
,
we have
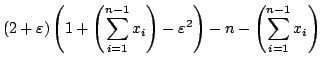 for
for ![]() .
As
.
As 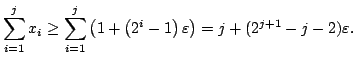 , we get
, we get
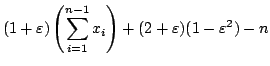 |
|||
Under the assumptions of Lemma 2 we
can now prove the following.
![]()
We may assume that
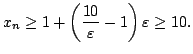
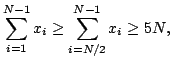 is large enough and
is large enough and 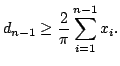
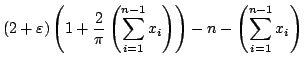
To conclude the proof, we consider a diameter ![]() large
enough for Lemma 3 to hold, so we have a lower
bound of 5 on the average size for the first
large
enough for Lemma 3 to hold, so we have a lower
bound of 5 on the average size for the first 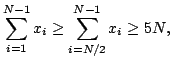 steps.
This suffices to show that all following steps are at
least of length 5.
steps.
This suffices to show that all following steps are at
least of length 5.
Again we proceed by induction and consider
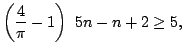
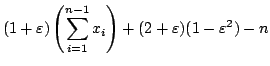 |
|||
With the help of these lemmas, we get
The preceding Lemmas 2, 3, 4
show that for any large enough ![]() , the sequence will consist of step lengths
that are all at least 5. This implies that the sequence will reach the
corner in a finite number of steps, showing that a competitive factor
of
, the sequence will consist of step lengths
that are all at least 5. This implies that the sequence will reach the
corner in a finite number of steps, showing that a competitive factor
of
 can be reached.
can be reached.
![]()
ARRAY(0x9264af0)ARRAY(0x9264af0)ARRAY(0x9264af0)ARRAY(0x9264af0)