Ein randomisierter Approximationsalgorithmus für das Kunstausstellungsproblem

Banos et al. reduzieren das Kunstausstellungsproblem auf ein weiteres NP-vollständiges, nämlich das Set-Cover Problem [28,29,30]. Es ist wie folgt definiert [47]:

Set-Cover:

Instanz:

Ein Tupel $(X,F)$, wobei $X$ eine beliebige endliche Menge ist. $F$ ist eine Teilmenge der Potenzmenge von $X$, also $F \subset \mathfrak{P}(X)$ und es gilt $X = \bigcup_{s \in F} s$.

Frage:

Bestimme $C \subset F$, so dass $X = \bigcup_{s \in C}$ gilt und $C$ minimale Kardinalität hat. $C$ ist also die minimale Menge, die alle Elemente von $X$ überdeckt.

Die Reduktion auf das Set-Cover Problem geschieht randomisiert. Der Roboter ist mit einer Karte seiner Umgebung ausgestattet. Im ersten Schritt des Algorithmus erfolgt die Generierung einer relativ großen Menge von Kandidatenpositionen. Dabei werden die Positionen zufällig ermittelt. Zudem besitzt jeder Punkt innerhalb der Karte die gleiche Wahrscheinlichkeit. Anschließend wählt der Algorithmus aus dieser Menge der Kandidatenpositionen eine minimale Menge, so dass die ganze Karte überblickt wird. Damit ist das Problem auf Set-Cover reduziert, d.h. $X$ ist die Karte und die Menge $F$ enthält die Teile der Karte, die von den Kandidatenpositionen überschaut werden können. Der randomisierte Approximationsalgorithmus ist:

Schritt 2 dieses Algorithmus ermöglicht, dass Eigenschaften von realen Sensoren, wie beispielsweise minimaler und maximaler Abstand zu Objekten oder Öffnungswinkel, berücksichtigt werden können.

Im dritten Schritt muss ein NP-vollständiges Problem gelöst werden. Glücklicherweise gibt es einen Greedy-Approximationsalgorithmus dafür, der sehr gute Ergebnisse liefert. Folgende Schritte werden bei einer Eingabe von $(X,F)$ ausgeführt:

Durch die Schleife hat der Algorithmus eine Laufzeit von $\O(\vert X\vert \, \vert F\vert \, \min(\vert X\vert \,\vert F\vert ))$. Nach [14] gibt es sogar eine Implementation, die nur lineare Zeit benötigt. Die Approximation mittels Greedy-Algorithmus liefert Ergebnismengen, deren Anzahl nicht sehr viel größer als das optimale Set-Cover ist [14]. Der folgende Satz gibt darüber Auskunft, doch zuvor muss die Approximationsgüte (engl.: approximation ratio) definiert werden. Man sagt, ein Approximationsalgorithmus für ein Problem hat die Approximationsgüte $\varrho (n)$, wenn für jede Instanz der Größe $n$ die Kosten $C$ der Lösung, die der Algorithmus liefert, innerhalb des Faktors $\varrho (n)$ der Kosten $C^*$ der optimalen Lösung liegen [14]:

$$\max\left(\frac{C}{C^*},\frac{C^*}{C}\right) \leq \varrho (n).$$

Satz 4 (Approximationsgüte von Set-Cover)   Der Greedy-Algorithmus für Set-Cover hat eine Approximationsgüte von $(\ln(\vert X\vert) + 1)$.

Beweis:Siehe [14] oder [47]. $\Box$

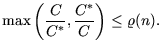Nachdem die optimalen Scanpositionen bei gegebener Karte approximiert worden sind, müssen diese vom Roboter nacheinander angefahren werden. Dieses Problem entspricht demjenigen des Handlungsreisenden (engl.: Travelling Salesman Problem).

TSP (euklidisch):

Instanz:

Eine Menge von Wegpunkten in der Ebene $U = \{u_1,\ldots,u_n\} \subset \mathbbm{R}^2$ mit $u_i = (x_i, y_i)$.

Frage:

Bestimme eine Permutation $\sigma$ über der Menge $\{1,\ldots,n\}$, so dass die Summe der Strecke $\sum_{i=1}^{n-1}d(u_{\sigma(i)},u_{\sigma(i+1)}) + d(u_{\sigma(n)},u_{\sigma(1)})$ minimal ist.

Dieses Problem ist ebenfalls NP-vollständig, lässt sich aber auch sehr gut approximieren [14,47].

Der nächste Abschnitt beschreibt den implementierten Algorithmus zum Finden der optimalen nächsten Scanposition. Er basiert auf Ideen aus obigem Approximationsalgorithmus. Dabei werden Kandidatenpunkte in die bereits explorierte Umgebung gestreut und anschließend ähnlich dem Greedy-Verfahren der Punkt ausgewählt, der den größen Informationsgewinn verspricht. Da der Roboter aber in diesem Fall keine vollständige Karte der Umgebung hat, handelt es sich um ein Explorationsproblem. Die dreidimensionale Umgebung des Roboters soll vollständig erfasst werden.