Die optimale nächste Scanposition soll berechnet werden, ohne dass der Roboter über eine vollständige Karte seiner Umgebung verfügt. Daraus folgt, dass zuerst die Umgebung des Roboters gescannt werden muss und dann die aufgenommenen Scans als Ausgangspunkt für die Berechnung dienen.
Der erste Schritt des Algorithmus besteht in der Aufnahme eines
3D-Scans. Anschließend wird aus den aufgenommenen Daten ein
so genanntes Riss-Polygon generiert. Ein Riss-Polygon repräsentiert
einen Schnitt durch die Roboterumgebung (Aufriss) und besteht aus
detektierten und hinzugefügten Linien. Jenseits dieser hinzugefügten
Linien befindet sich noch nicht explorierte Umgebung. Zur Erzeugung
des Riss-Polygons werden alle Messpunkte herausgefiltert, die sich
auf einer definierten Höhe befinden. Abbildung 4.4 (oben)
verdeutlicht dies; es werden alle Punkte ermittelt, die eine Höhe von
150cm ![]() 2cm aufweisen.
2cm aufweisen.
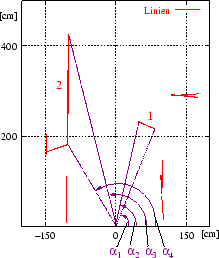
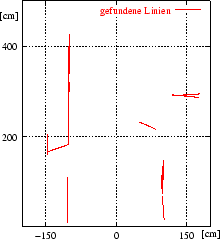
Die derart bestimmten Punkte dienen als Eingabe für einen Linienerkenner. Da die Punkte nicht sortiert sind - sie stammen aus unterschiedlichen Scanschnitten -, kommt die Hough-Transformation [74,75] zum Einsatz. Ihr Ergebnis ist in Abbildung 4.4 (unten links) zu sehen. Die detektierten Linien verbindet der Algorithmus nun so, dass ein Polygon entsteht. Zwischen den Sprungkanten (vgl. Kapitel 3.4) werden Linien eingeführt, die einen Teil des Risses der zugrunde liegenden Höhe verdecken; d.h. dass sich ein Teil der Umgebung hinter dieser Linie befindet, aber noch nicht gescannt wurde. Wenn die Linien sortiert vorliegen, ist es einfach, sie richtig zu verbinden. Der kleinste Winkel zwischen den Endpunkten einer Linie und der Scannerposition dient dabei als Sortierkriterium. Abbildung 4.3 verdeutlicht diesen Vorgang.
|
Die Art und Weise, wie die detektierten Linien verbunden werden,
entspricht dem Vorgehen von so genannten
Sweepline-Algorithmen. Eine analoge Sichtweise
besteht darin, einen Strahl von der Scannerposition aus von rechts
nach links laufen zu lassen (also über alle möglichen Werte von
![]() ). Falls der Strahl auf eine Linie trifft, wird diese mit der
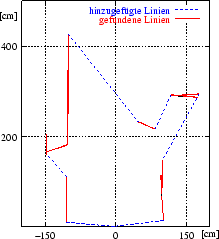
Vorgängerlinie verbunden. Das Riss-Polygon entsteht durch das
Verbinden aller detektierten Linien (vgl. Abbildung 4.4
unten rechts).
). Falls der Strahl auf eine Linie trifft, wird diese mit der
Vorgängerlinie verbunden. Das Riss-Polygon entsteht durch das
Verbinden aller detektierten Linien (vgl. Abbildung 4.4
unten rechts).
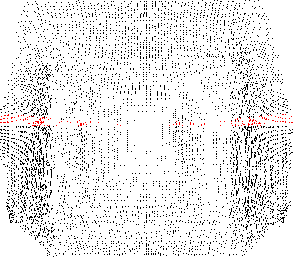
|
Der zweite Schritt des Algorithmus zur Berechnung der optimalen nächsten Scanposition erzeugt Kandidatenpositionen innerhalb des Riss-Polygons (vgl. Abbildung 4.5 links). Alle Positionen innerhalb des Polygons haben die gleiche Wahrscheinlichkeit. Die Aufgabe besteht nun darin, diejenige Kandidatenposition auszuwählen, an der ein weiteres Scannen den maximalen Zuwachs an Information verspricht. Möglichst viele Messpunkte des 3D-Scanners sollen in Richtung verdeckter, also hinzugefügter Kanten liegen.
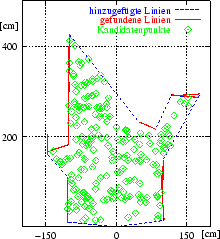
|
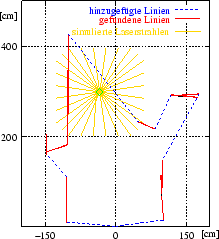
Der dritte Schritt evaluiert die Kandidatenpunkte (vgl. Abbildung 4.5 rechts). Für jeden dieser Punkte muss errechnet werden, welcher Anteil vom Riss-Polygon sichtbar ist. In der implementierten Fassung geschieht dies über eine Simulation des Laserscanners. Von der Kandidatenposition aus werden virtuelle Laserstrahlen ausgesendet, und die Anzahl der Schnittpunkte wird mit detektierten bzw. mit hinzugefügten Linien bestimmt. Entscheidend für eine Kandidatenposition ist dabei die Anzahl der Schnittpunkte mit den hinzugefügten Linien. Bei der Bestimmung der Schnittpunkte finden die physikalischen Eigenschaften des Sensors Berücksichtigung. Schnittpunkte, die zu nah am Sensor liegen, werden nicht gezählt. Gleiches gilt für zu große Entfernungen vom Laserscanner.
An dieser Stelle bezieht der Planungsalgorithmus die dritte Dimension
ein. Der 3D-Laserscanner ist fest in einer Höhe von 105 cm auf dem
Roboter montiert. Wenn der Scanner Objekte in einer anderen Höhe
erfassen will, muss er einen Mindestabstand einhalten. Die Ursache
dafür liegt im Öffnungswinkel des Sensors (![]() 90
90![]() )
(vgl. Abbildung 4.6). Des Weiteren nimmt die Strahldichte mit
dem Quadrat der Entfernung ab [54]. Daraus folgt: Je weiter
der Scanner vom Objekt entfernt steht, desto weniger Laserstrahlen
treffen auf das Objekt. Optimal ist daher eine Scannerposition nahe
dem Objekt, aus der es gerade noch erfasst werden kann.
)
(vgl. Abbildung 4.6). Des Weiteren nimmt die Strahldichte mit
dem Quadrat der Entfernung ab [54]. Daraus folgt: Je weiter
der Scanner vom Objekt entfernt steht, desto weniger Laserstrahlen
treffen auf das Objekt. Optimal ist daher eine Scannerposition nahe
dem Objekt, aus der es gerade noch erfasst werden kann.

|
Die Mindestentfernung ![]() , die der 3D-Scanner vom Objekt bzw. den
Kanten der Riss-Ebene haben muss, lässt sich aus der Höhe des
Scanners
, die der 3D-Scanner vom Objekt bzw. den
Kanten der Riss-Ebene haben muss, lässt sich aus der Höhe des
Scanners ![]() und der Riss-Ebene
und der Riss-Ebene ![]() errechnen. (vgl. Abbildung
4.6). Falls das zu scannende Objekt unterhalb der Höhe des
Scanners liegt, ist
errechnen. (vgl. Abbildung
4.6). Falls das zu scannende Objekt unterhalb der Höhe des
Scanners liegt, ist
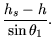 |
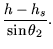 |
Nachdem alle Kandidatenpunkte unter Berücksichtigung der minimalen
Entfernung ![]() und einer maximalen Entfernung evaluiert sind, wird
die beste Orientierung des Roboters am Kandidatenpunkt bestimmt. Dabei
versucht der Roboter in den größten noch nicht gesehenen Bereich zu
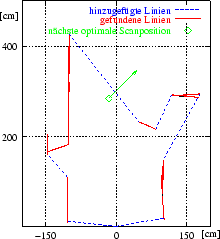
schauen. Das Ergebnis des Algorithmus für die Riss-Ebene aus
Abbildung 4.4 ist in Abbildung 4.7
angegeben.
und einer maximalen Entfernung evaluiert sind, wird
die beste Orientierung des Roboters am Kandidatenpunkt bestimmt. Dabei
versucht der Roboter in den größten noch nicht gesehenen Bereich zu
schauen. Das Ergebnis des Algorithmus für die Riss-Ebene aus
Abbildung 4.4 ist in Abbildung 4.7
angegeben.
Die optimale nächste Scanposition besitzt drei Eigenschaften: Erstens
ist der bei der Evaluierung jedes NBV-Kandidatenpunktes ![]() errechnete
Wert
errechnete
Wert ![]() gleich der Anzahl der Schnittpunkte mit hinzugefügten
Linien. Zweitens sollte die Position nicht allzu weit von der aktuellen
Position entfernt sein. Und drittens ist ein ständiges Drehen des
Roboters zu vermeiden. Die folgende Formel trägt dem Rechnung und
definiert dadurch den Begriff ,,optimale nächste Scanposition``:
gleich der Anzahl der Schnittpunkte mit hinzugefügten
Linien. Zweitens sollte die Position nicht allzu weit von der aktuellen
Position entfernt sein. Und drittens ist ein ständiges Drehen des
Roboters zu vermeiden. Die folgende Formel trägt dem Rechnung und
definiert dadurch den Begriff ,,optimale nächste Scanposition``:
Wendet man das oben beschriebene Verfahren auf Riss-Ebenen verschiedener Höhe an, lässt sich die optimale nächste Scanposition für den 3D-Laserscanner bestimmen. Es gibt Situationen, in denen Verdeckungen auftreten, die der 3D-Laserscanner nicht erfassen kann. Dies ist durch den Aufbau bedingt: Der Sensor hat eine feste Höhe.
|