Die optimale nächste Scanposition aus mehreren 3D-Scans.

Liegen mehrere 3D-Scans vor, muss aus diesen ein Riss-Polygon erstellt werden, um die optimale nächste Scanposition zu errechnen. Kapitel 3 beschreibt die Transformationen von 3D-Scans zum Aufbau einer konsistenten Szene. Aus jedem 3D-Scan entsteht ein separates Riss-Polygon. Alle erzeugten Risse befinden sich auf gleicher Höhe. Die Polygone werden mittels Vattis Polygon Clipping Algorithmus [83] zu einem einzigen Polygon vereinigt. Dabei verändert sich die Art der Kanten (detektierte bzw. hinzugefügte Kanten) nicht. Abbildung 4.8 veranschaulicht diesen Prozess.

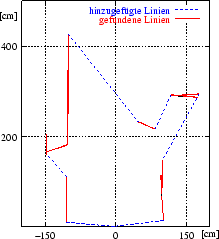
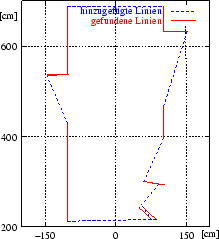
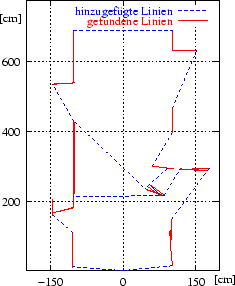
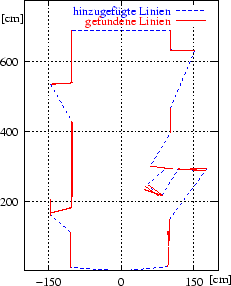
Der verwendete Polygon Clipping Algorithmus arbeitet nach einem Sweepline Verfahren. Die beiden Polygone tastet man dabei durch horizontale Streifen ab. Die Streifen entstehen durch aufeinander folgende horizontale Strahlen durch alle Eckpunkte des Polygons. Bei diesem Durchlaufen der Polygone wird eine Tabelle aufgebaut, die alle Kantenzüge im aktuellen Streifen enthält. Mit Hilfe der Tabelle werden die im Streifen enthaltenen Ecken und Kanten klassifiziert. Anhand der Klassifizierung berechnet der Clipping Algorithmus die Vereinigung der beiden Polygone [83]. Das so entstandene neue Polygon dient als Basis für den randomisierten Approximationsalgorithmus.

Der alternative Weg zur Riss-Polygonerzeugung, zuerst verschiedene 3D-Scans auf Messdatenebene zu einem Metascan zu vereinigen, um anschließend mit einem Linienerkenner den sichtbaren Teil des Risses zu erzeugen, hat den Nachteil, dass der einfache Sweepline Algorithmus (vgl. Seite ) nicht funktioniert. Die Schwierigkeit besteht im Hinzufügen der verdeckten Kanten.

Abbildung: Das Zusammenfügen zweier Riss-Polygone; Oben: Zwei Polygone aus unterschiedlichen 3D-Scans, Unten: Die Vereinigung der beiden Polygone mittels Vattis Polygon Clipping Algorithmus.

Der NBV-Algorithmus lässt sich wie folgt zusammenfassen: