


Next: Das Anfahren der optimalen
Up: Die Berechnung der optimalen
Previous: Die optimale nächste Scanposition
Der erste Schritt des Algorithmus betrachtet
alle Messpunkte in einem 3D-Scan, um diejenigen Punkte zu filtern,
die sich auf der definierten Höhe befinden. Nach dem Filtern der
Punkte wird die Hough-Transformation eingesetzt, die eine Laufzeit
von
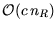 hat. Dabei bezeichnet
hat. Dabei bezeichnet 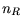 die Anzahl der Punkte
in der gewählten Riss-Ebene (
die Anzahl der Punkte
in der gewählten Riss-Ebene (
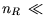 Anzahl aller Messdaten
in einem 3D-Scan) und
Anzahl aller Messdaten
in einem 3D-Scan) und 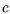 ist abhängig von der größten auftretenden
Entfernung vom 3D-Scanner. Die Polygonerzeugung wendet Bubble-Sort
auf die Linien an; die Anzahl der Linien ist allerdings wesentlich
kleiner als die Anzahl der Punkte in einer Riss-Ebene. Liegt bereits
ein Riss-Polygon vor, muss das neu erzeugte mit dem vorhandenen
vereinigt werden. Vattis Polygon Clipping Algorithmus hat eine
Laufzeit von
ist abhängig von der größten auftretenden
Entfernung vom 3D-Scanner. Die Polygonerzeugung wendet Bubble-Sort
auf die Linien an; die Anzahl der Linien ist allerdings wesentlich
kleiner als die Anzahl der Punkte in einer Riss-Ebene. Liegt bereits
ein Riss-Polygon vor, muss das neu erzeugte mit dem vorhandenen
vereinigt werden. Vattis Polygon Clipping Algorithmus hat eine
Laufzeit von 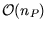 .
. 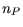 ist die Summe der Kanten beider
Riss-Polygone [83]. Die Anzahl der Kanten in einem
Riss-Polygon ist vor dem Clipping doppelt so groß wie die Anzahl der
detektierten Linien im Riss, d.h.
ist die Summe der Kanten beider
Riss-Polygone [83]. Die Anzahl der Kanten in einem
Riss-Polygon ist vor dem Clipping doppelt so groß wie die Anzahl der
detektierten Linien im Riss, d.h.
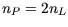 .
.
Dieser erste Schritt benötigt in der Ausführung auf einem PIII-600
weniger als eine Sekunde. Auch für den zweiten Schritt, das Erzeugen
der Kandidatenpositionen, genügt ein Bruchteil einer Sekunde. Der
dritte Schritt ist der zeitaufwendigste. Die Evaluation der
Kandidatenpunkte benötigt
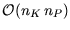 . Dabei ist
. Dabei ist 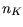 die Anzahl
der Kandidatenpunkte und
die Anzahl
der Kandidatenpunkte und 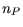 die der Kanten im Riss-Polygon.
Letztere steigt mit der Größe der explorierten Umgebung. Auch ist die
Simulation der Laserstrahlen aufwendig, da für jeden Strahl der zum
Scanner nächste Schnittpunkt mit den Kanten des Riss-Polygons
ermittelt werden muss. Die Durchführung des dritten Schrittes kann für
den Flur des FhG-AIS Gebäudes C2 bis zu 2 Sekunden (PIII-600) in
Anspruch nehmen.
die der Kanten im Riss-Polygon.
Letztere steigt mit der Größe der explorierten Umgebung. Auch ist die
Simulation der Laserstrahlen aufwendig, da für jeden Strahl der zum
Scanner nächste Schnittpunkt mit den Kanten des Riss-Polygons
ermittelt werden muss. Die Durchführung des dritten Schrittes kann für
den Flur des FhG-AIS Gebäudes C2 bis zu 2 Sekunden (PIII-600) in
Anspruch nehmen.



Next: Das Anfahren der optimalen
Up: Die Berechnung der optimalen
Previous: Die optimale nächste Scanposition
Andreas Nüchter
2002-07-10
![]() . Dabei ist
. Dabei ist ![]() die Anzahl
der Kandidatenpunkte und
die Anzahl
der Kandidatenpunkte und ![]() die der Kanten im Riss-Polygon.
Letztere steigt mit der Größe der explorierten Umgebung. Auch ist die
Simulation der Laserstrahlen aufwendig, da für jeden Strahl der zum
Scanner nächste Schnittpunkt mit den Kanten des Riss-Polygons
ermittelt werden muss. Die Durchführung des dritten Schrittes kann für
den Flur des FhG-AIS Gebäudes C2 bis zu 2 Sekunden (PIII-600) in
Anspruch nehmen.
die der Kanten im Riss-Polygon.
Letztere steigt mit der Größe der explorierten Umgebung. Auch ist die
Simulation der Laserstrahlen aufwendig, da für jeden Strahl der zum
Scanner nächste Schnittpunkt mit den Kanten des Riss-Polygons
ermittelt werden muss. Die Durchführung des dritten Schrittes kann für
den Flur des FhG-AIS Gebäudes C2 bis zu 2 Sekunden (PIII-600) in
Anspruch nehmen.