Kantenbasiertes Scanmatching

Sappa et al. schlagen ein merkmalbasiertes Scanmatching auf der Grundlage des ICP-Algorithmus vor [65]. Dabei sind die extrahierten Merkmale die Kanten in einem Scan. Um diese Kanten zu finden, zerlegen Sappa et al. einen 3D-Scan in horizontale und vertikale Schnitte und suchen dort nach Diskontinuitäten. Dabei unterscheiden sie so genannte Faltenkanten (engl.: crease edge) und Sprungkanten (engl.: jump edge). Faltenkanten entstehen durch die Änderung der Orientierung einer Fläche; die Ursache der Sprungkanten liegt im großen Abstand benachbarter Scanpunkte. Die Punkte in einem Schnitt werden durch quadratische Funktionen approximiert, wodurch Sappa et al. die zwei Kantentypen erkennen. Das Zerlegen eines 3D-Scans in horizontale und vertikale Schnitte garantiert, dass alle Kantenpunkte gefunden werden. Der ICP-Algorithmus registriert anschließend die Kantenpunkte, d.h. es kommt nur eine Teilmenge der vorhandenen Datenpunkte zum Einsatz.

Abbildung 3.7: Liniendarstellung eines 3D-Scans und Kantenextraktion.

Der in dieser Arbeit eingesetzte Laserscanner (Abbildung 2.4) scannt jeweils eine Ebene, in der Linien erkannt werden. Die Endpunkte der Linien gehören entweder zu den Faltenkanten oder zu den Sprungkanten (vgl. Abbildung 3.7). Durch die Drehbewegung werden fast alle Kantenpunkte gefunden, eine zusätzliche Zerlegung der Scanpunkte in vertikale Schnitte erscheint nicht nötig. Die Abbildung 3.8 zeigt die auf der Basis von Linienerkennung extrahierten Kantenpunkte und stellt die Ergebnisse der beiden in Kapitel 2.4.2 vorgestellten Linienerkenner gegenüber. Es wird deutlich, dass die mit Hough-Transformation erzeugten Kantenpunkte weniger stark verrauscht sind. Dies lässt sich auf die qualitativ besseren Linien der Hough-Transformation zurückführen.

Abbildung 3.8: Kantenpunkte: Links: Matching-Algorithmus. Rechts: Hough-Transformation.

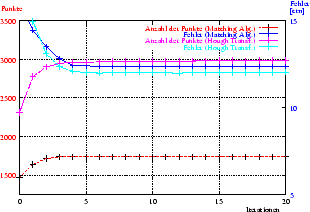
Es liegt nahe, den ICP-Algorithmus auf diese Punkte anzuwenden. Die 46080 Punkte des Beispielscans enthalten 3704 Kantenpunkte. Damit hat dieses Verfahren eine etwas bessere Performanz als die Verwendung der REDUZIERTEN PUNKTE (Datenreduktion etwa 1:12). Tabelle 3.3 und Abbildung 3.9 zeigen die Ergebnisse. Die angegebene Zeit setzt sich aus der für den ICP benötigten Zeit und jener, die für die Linienerkennung gebraucht wird, zusammen. Es dominiert der Aufwand für die Linienerkennung (Matching Algorithmus: 4s, Hough-Transformation: 2min 45s). Der hohe Aufwand bei der Hough-Transformation erklärt sich dadurch, dass sich der Bereich, auf dem Linien erkannt werden müssen, schlecht einschränken lässt, da von möglichst vielen Kantenpunkten der Scans Punktpaare gebildet werden sollen. Es ist eine Linienerkennung in einem Radius von 10 Metern nötig, um die Scans zu matchen, während die Hough-Transformation als online Algorithmus nur Punkte im Abstand von 5 Metern betrachtet [74,75].

Tabelle 3.3: Vergleich der Methoden zur Bildung von Kantenpunktpaaren, Zeiten bei brute-force Suche und vollständiger Datenverarbeitung sowie Anteil für das Scanmatching (in Klammern). Ausgangsposition des ICP-Algorithmus ist die auf Odometrie-Daten beruhende Roboterposition $(x,y,\theta) = (27.10,\ 233.20,\ 6.64)$.

Methode	Zeit	Iterationen	Fehler	Endkoordinaten
V - Kantenpunkte (Matching Alg.)	6s ($<$2s)	20	12.37	(6.41, 227.92, -0.41)
VI - Kantenpunkte (Hough Transf.)	2m 48s ($3$s)	50	13.20	(0.06, 221.81, -2.03)

Abbildung: Die Entwicklung des mittleren Fehlers und die Anzahl der Kantenpunktpaare während des ICP-Algorithmus