Die vorangehenden Teile dieses Kapitels haben sich mit dem Matching
von zwei 3D-Scans beschäftigt. Erst eine Registrierung vieler Scans
erlaubt aber oftmals das vollständige Erfassen von Szenen. Daher wird
im Folgenden das Matching mehrerer 3D-Scans behandelt. Die
Registrierung von ![]() Punktmengen zu einem konsistenten Modell ist
aktuelles Forschungsgebiet, in dem bereits einige Lösungsansätze
präsentiert wurden
[8,11,16,19,58,72]:
Punktmengen zu einem konsistenten Modell ist
aktuelles Forschungsgebiet, in dem bereits einige Lösungsansätze
präsentiert wurden
[8,11,16,19,58,72]:
Diese einfache Methode liefert eine Registrierung aller Scans unter der Voraussetzung, dass aufeinander folgende 3D-Scans genügend überlappen. Damit auch große Positions- oder Orientierungsänderungen des Roboters berücksichtigt werden können, wird in der implementierten Fassung dieses Algorithmus in einem Vorverarbeitungsschritt derjenige 3D-Scan mit dem größten Überlappungsbereich zu dem zu registrierenden Scan ermittelt. Der so bestimmte Scan dient dann als Basis für den zu matchenden Scan.
Bei einem solchen paarweisen Matching kumulieren Fehler. Da das Scanmatching vorangegangener Scans niemals perfekt sein kann, wird dieser Fehler an die nachfolgenden Scans weitergegeben. Anschließend entstehende Registrationsfehler addieren sich zu den vorangegangenen.
Ein weiteres potenzielles Problem des inkrementellen Matchings ist in Abbildung 3.10 illustriert. Mehrere Scans sind zu einem Metascan zusammengefügt, es entsteht eine Schale begrenzter Dicke (Abbildung 3.10 (a)). Bei der Registrierung eines weiteren Scans wäre es wünschenswert, diesen in der Mitte der bereits vorhandenen Scans zu platzieren (Abbildung 3.10(b)). Je nach Implementation ist es wahrscheinlicher, dass der neue Scan sich an die äußere Schale anlagert. Dadurch verbreitert sich die Dicke der Schale von Scan zu Scan [58].
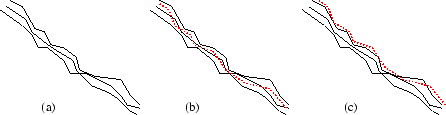
|
Die beiden vorangegangenen Verfahren haben einen entscheidenden Nachteil: Wenn zusätzliche Scans hinzugefügt werden, besteht die Möglichkeit, dass diese neuen Scans Informationen mitbringen, die das bisherige Matching verbessern [58]. Dies wird erst in dem nachfolgend vorgestellten Verfahren berücksichtigt, das zusätzlich den entstehenden Registrationsfehler gleichmäßig über alle Scans verteilt.
Benjemaa und Schmitt verwenden folgenden sequenziellen Algorithmus, um das Problem des Matchings mehrerer 3D-Scans zu lösen [8]:

Eggert et al. [19] und Stoddart/Hilton [72] benutzen eine ähnliche Methode. Sie paaren jeden Punkt eines Scans mit dem nächsten Punkt. Dabei suchen sie in allen weiteren Scans. Anschließend berechnen sie die Transformation simultan; ihr Algorithmus simuliert ein virtuelles (und vereinfachtes) dynamisches System aus gespannten Federn (vgl. Kapitel 3.3.3). Sie arbeiten nicht mit der besten Transformation weiter, um somit Fehler zu minimieren, deren Ursachen in falschen Punktpaaren liegen [19,72].
Das implementierte simultane Matching ist vergleichbar mit dem Algorithmus von Benjemaa und Schmitt, basiert aber zusätzlich auf Ideen von Pulli [58]. Das Verfahren registriert die Scans in der Reihenfolge, in der sie aufgenommen wurden, fügt also einer Menge von Scans jeweils einen weiteren hinzu. Die wesentlichen Schritte des Algorithmus sind:
