|
Wie der Name schon sagt, handelt es sich bei der Datenstruktur Octalbaum um einen Baum, also einen kreisfreien Graphen[45]. Jeder innere Knoten des Baumes besitzt acht Nachfolgerknoten. Die Blätter haben keine Nachfolger, enthalten aber die im Baum gespeicherten Daten. Die Idee besteht nun darin, die Messdaten in den Blättern eines Octalbaumes zu speichern.
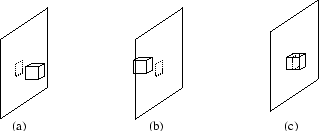
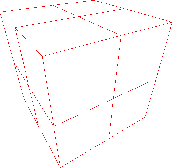
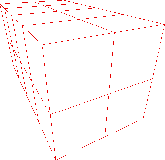
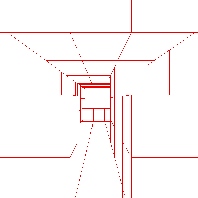
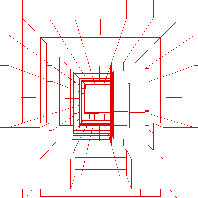
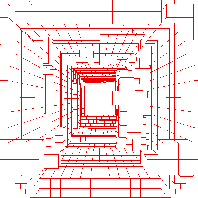
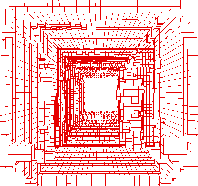
Alle Datenpunkte können von einem Quader umschlossen werden, der die Wurzel des Octalbaumes darstellt und entlang der Achsen des Koordinatensystems ausgerichtet ist. Durch das Einfügen von 3 Ebenen (horizontal, vertikal und in der Flucht) wird der Quader in kleinere, gleichgroße Quader zerteilt. Danach werden die Daten auf die kleineren Quader verteilt. Für diese ermittelt man, ob sie die Oberfläche eines Objekte enthalten. Abbildung 5.3 zeigt die drei dabei zu unterscheidenden Fälle: Ein Quader kann vor, hinter oder auf der Oberfläche liegen. Leere Quader gehören sicherlich nicht zur Oberfläche des Objektes. An diesen Stellen schneidet man den Baum ab und bestimmt keine Nachfolgerknoten. Die Quader, die zum Objekt gehören, werden wiederum durch das Einfügen von 3 Ebenen in acht kleinere zerlegt. Diese Rekursion erzeugt an den Blättern Quader, die die Oberfläche der Objekte, auf denen die Messdaten liegen, approximieren. Abbildung 5.4 zeigt den beschriebenen Prozess. Das Verfahren funktioniert unabhängig von den einzelnen 3D-Scans und der Struktur der Daten darin, da es ausschließlich Messpunkte verwendet.

|

|