

Next: Data Reduction
Up: Range Image Registration and
Previous: Matching as Optimization
To digitalize environments, multiple 3D scans have to be
registered. After registration, the scene has to be globally
consistent. A straightforward method for aligning several 3D
scans is pairwise matching, i.e., the new scan is
registered against the scan with the largest overlapping
areas. The latter one is determined in a preprocessing step.
Alternatively, Chen and Medioni [7] introduced an
incremental matching method, i.e., the new scan is
registered against a so-called metascan, which is the
union of the previously acquired and registered scans. Each scan
matching has a limited precision. Both methods accumulate the
registration errors such that the registration of many scans
leads to inconsistent scenes and to problems with the robot
localization.
Pulli presents a registration method that minimizes the global
error and avoids inconsistent scenes [19]. This
method distributes the global error while the registration of one
scan is followed by registration of all neighboring scans. Other
matching approaches with global error minimization have been
published, e.g., by Benjemaa et. al. [4] and
Eggert et. al. [9].
Based on the idea of Pulli we have designed a method called
simultaneous matching [17,22]. Thereby, the
first scan is the master scan and determines the coordinate
system. This scan is fixed. The following steps register all
scans and minimize the global error:
- Based on the robot odometry, pairwise matching is used to find a
start registration for a new scan. This step speeds up
computation.
- A queue is initialized with the new scan.
- Three steps are repeated until the queue is empty:
- The current scan is the first scan of the queue. This scan is removed
from the queue.
- If the current scan is not the master scan, then a set of
neighbors (set of all scans that overlap with the current scan)
is calculated. This set of neighbors forms one point set
 . The
current scan forms the data point set
. The
current scan forms the data point set 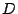 and is aligned with the
ICP algorithms.
and is aligned with the
ICP algorithms.
- If the current scan changes its location by applying the
transformation (translation or rotation), then each single scan
of the set of neighbors that is not in the queue is added to the
end of the queue.
Note: One scan overlaps with another iff more than 250
corresponding point pairs exist.
In contrast to Pulli's approach, the proposed method is totally
automatic and no interactive pairwise alignment has to be done.
Furthermore the point pairs are not fixed [19]. The
accumulated alignment error is spread over the whole set of
acquired 3D scans. An explicit detection of closed loops for the
proposed solution to the SLAM problem is not necessary, multiple
overlapping 3D scans are sufficient to diffuse the alignment
error equally over the set of 3D scans.


Next: Data Reduction
Up: Range Image Registration and
Previous: Matching as Optimization
root
2004-03-04
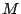 . The
current scan forms the data point set
. The
current scan forms the data point set 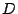 and is aligned with the
ICP algorithms.
and is aligned with the
ICP algorithms.