The computational expense of the ICP algorithm depends mainly on
the number of points. In a brute force implementation the point
pairing is in ![]() . Data reduction reduces the time required
for matching. Several approaches have been presented for
subsampling the data, including randomized sampling, uniform
sampling, normal-space sampling and covariance sampling
[20,12]. Randomized sampling selects points
at random, uniform sampling draws samples equally distributed
samples from the input point cloud. Normal space sampling, as
proposed by Rusinkiewicz and Levoy, aims at constraining
translational sliding of input meshes, generated from the point
cloud [20]. Their algorithm tries to ensure that the
normals of the selected points uniformly populate the sphere of
directions. Covariance sampling as proposed by Levoy et al. and
extends the nomal space approach. They identify whether a pair of
meshes will be unstable in the ICP algorithms by estimating a
covariance matrix from a sparse uniform sampling of the input
[12].
. Data reduction reduces the time required
for matching. Several approaches have been presented for
subsampling the data, including randomized sampling, uniform
sampling, normal-space sampling and covariance sampling
[20,12]. Randomized sampling selects points
at random, uniform sampling draws samples equally distributed
samples from the input point cloud. Normal space sampling, as
proposed by Rusinkiewicz and Levoy, aims at constraining
translational sliding of input meshes, generated from the point
cloud [20]. Their algorithm tries to ensure that the
normals of the selected points uniformly populate the sphere of
directions. Covariance sampling as proposed by Levoy et al. and
extends the nomal space approach. They identify whether a pair of
meshes will be unstable in the ICP algorithms by estimating a
covariance matrix from a sparse uniform sampling of the input
[12].
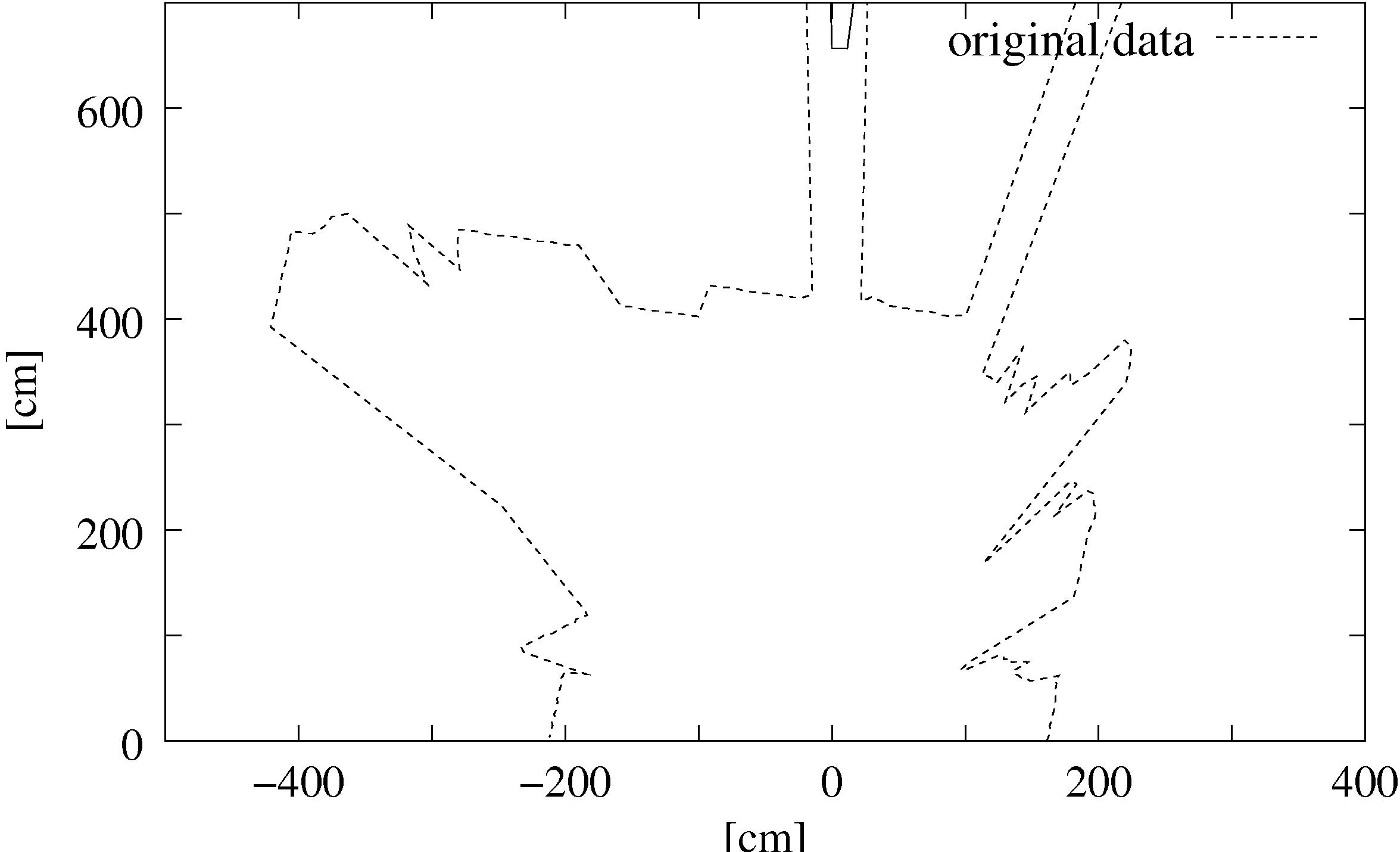
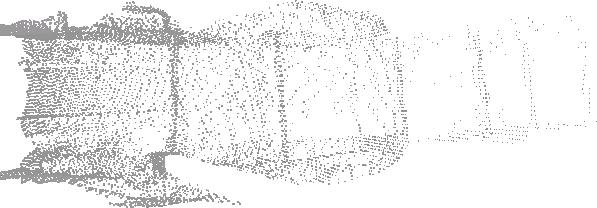
The data reduction proposed here considers the procedure of the scanning process, i.e., the spherical and continuous measurment of the laser. Scanning is noisy and small errors may occur. Two kinds of errors mainly occur: Gaussian noise and so called salt and pepper noise. The latter one occurs for example at edges, where the laser beam of the scanner hits two surfaces, resulting in a mean and erroneous data value. Furthermore reflections lead to suspicious data. Without filtering, only a few outliers lead to multiple wrong point pairs during the matching phase and results in an incorrect 3D scan alignment.
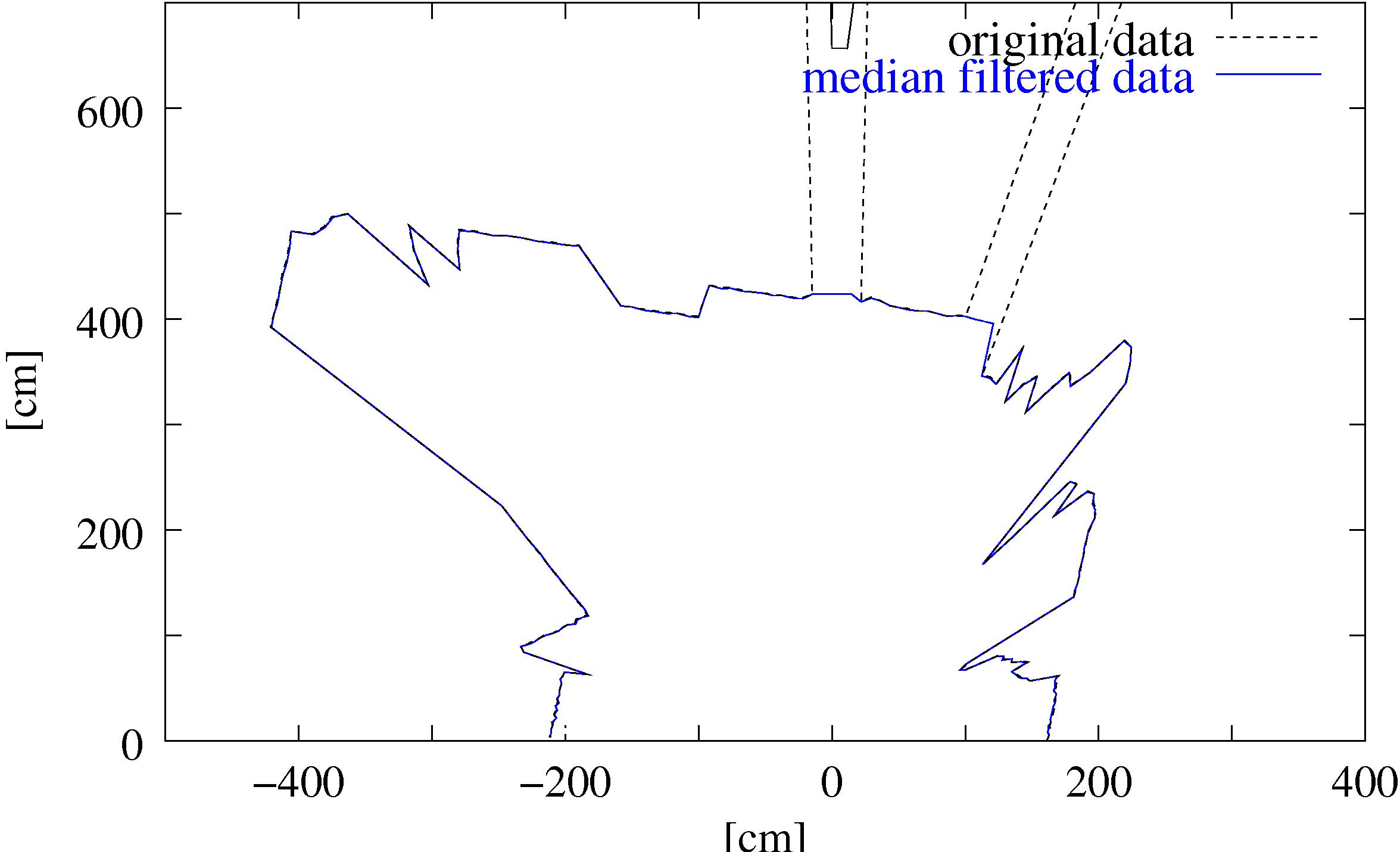
We propose a fast filtering method to reduce and smooth the data
for the ICP algorithm. The filter is applied to each 2D scan
slice, containing 361 data points. It is a combination of a
median and a reduction filter. The median filter removes the
outliers (Fig. 3) by replacing a data point with the
median value of the ![]() surrounding points (here:
surrounding points (here: ![]() ). The
neighbor points are determined according to their number within
the 2D scan, since the laser scanner provides the data sorted in
a counter-clockwise direction. The median value is calculated
with regards to the Euclidian distance of the data points to the
point of origin. In order to remove salt and pepper noise but
leave the remaining data untouched, the filtering algorithm
replaces a data point with the corresponding median value if and
only if the difference (Euclidian distance) between both is
larger than a fixed threshold (here: threshold = 200 cm).
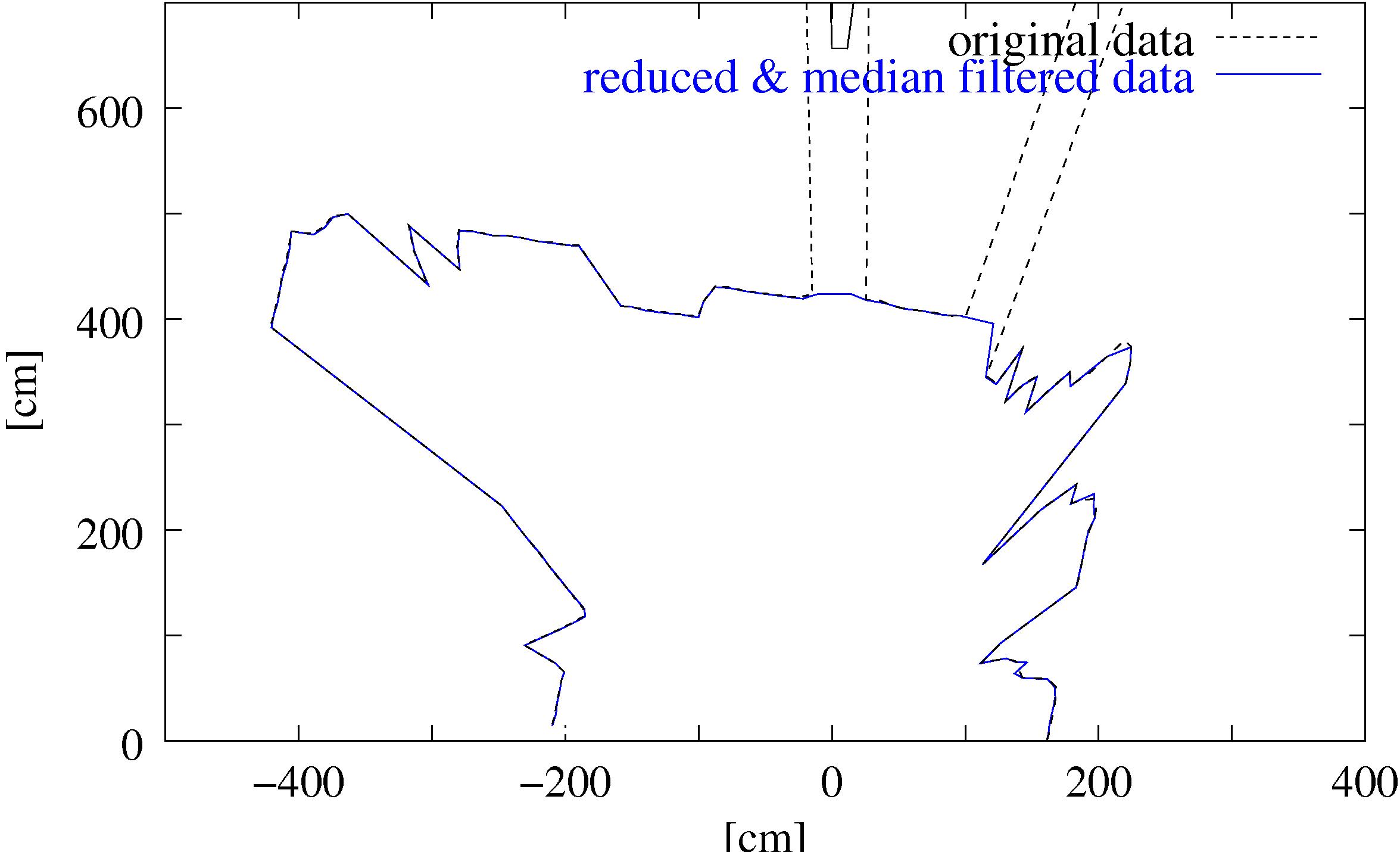
The data reduction works as follows: The scanner emits the laser
beams in a spherical way, such that the data points close to the
source are more dense. Multiple data points located close
together are joined into one point. This reduction lowers the
Gaussian noise. The number of these so called reduced
points is in the mine application one order of magnitude smaller
than the original one (Fig. 3). Finally the data
points of a slice have a minimal distance of 10 cm and
approximate the surface. The clue of the algorithm is that it is
nearly impossible to detect differences between the median
filtered and the reduced data (Fig. 3). The reduction
fulfills the sampling criterions stated by Boulanger et
al. [6], i.e., sampling the range images, such
that the surface curvature is maintained.
). The
neighbor points are determined according to their number within
the 2D scan, since the laser scanner provides the data sorted in
a counter-clockwise direction. The median value is calculated
with regards to the Euclidian distance of the data points to the
point of origin. In order to remove salt and pepper noise but
leave the remaining data untouched, the filtering algorithm
replaces a data point with the corresponding median value if and
only if the difference (Euclidian distance) between both is
larger than a fixed threshold (here: threshold = 200 cm).
The data reduction works as follows: The scanner emits the laser
beams in a spherical way, such that the data points close to the
source are more dense. Multiple data points located close
together are joined into one point. This reduction lowers the
Gaussian noise. The number of these so called reduced
points is in the mine application one order of magnitude smaller
than the original one (Fig. 3). Finally the data
points of a slice have a minimal distance of 10 cm and
approximate the surface. The clue of the algorithm is that it is
nearly impossible to detect differences between the median
filtered and the reduced data (Fig. 3). The reduction
fulfills the sampling criterions stated by Boulanger et
al. [6], i.e., sampling the range images, such
that the surface curvature is maintained.
The data for the scan matching is collected from every third scan slice. This fast vertical reduction yields a good surface description. Data reduction and filtering are online algorithms and run in parallel to the 3D scanning.
|


|