In every iteration the optimal transformation (![]() ,
, ![]() )
has to be computed. Eq. (
)
has to be computed. Eq. (![]() ) can be reduced to
) can be reduced to
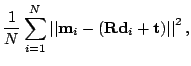 , since the
correspondence matrix can be represented by a vector containing
the point pairs.
, since the
correspondence matrix can be represented by a vector containing
the point pairs.
In earlier work [10] we used a quaternion based method
[3], but the following one, based on singular value
decomposition (SVD), is robust and easy to implement, thus we give a
brief overview of the SVD based algorithms. It was first published by
Arun, Huang and Blostein [2]. The difficulty of this
minimization problem is to enforce the orthonormality of matrix ![]() . The first step of the computation is to decouple the calculation
of the rotation
. The first step of the computation is to decouple the calculation
of the rotation ![]() from the translation
from the translation ![]() using the centroids
of the points belonging to the matching, i.e.,
using the centroids
of the points belonging to the matching, i.e.,
Theorem: The optimal rotation is calculated
by
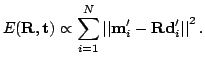 . Herby the matrices
. Herby the matrices ![]() and
and ![]() are
derived by the singular value decomposition
are
derived by the singular value decomposition
![]() of a correlation matrix
of a correlation matrix ![]() . This
. This
![]() matrix
matrix
![]() is given by
is given by
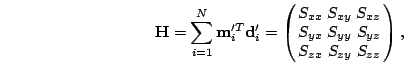 . The analogous
algorithm is derived directly from this theorem.
. The analogous
algorithm is derived directly from this theorem.
Finally, the optimal translation is calculated using
eq. ![]() ) (see also (
) (see also (![]() )).
)).