Next: Computing the Optimal Rotation
Up: 3D Mapping with Semantic
Previous: Extracting Semantic Information
Scan Registration and Robot Relocalization
Multiple 3D scans are necessary to digitalize environments without
occlusions. To create a correct and consistent model, the scans have
to be merged into one coordinate system. This process is called
registration. If the localization of the robot with the 3D scanner
were precise, the registration could be done directly based on the
robot pose. However, due to the unprecise robot sensors, self
localization is erroneous, so the geometric structure of overlapping
3D scans has to be considered for registration. Furthermore, Robot
motion on natural surfaces has to cope with yaw, pitch and roll
angles, turning pose estimation into a problem in six mathematical
dimensions. A fast variant of the ICP algorithm registers the 3D scans
in a common coordinate system and relocalizes the robot. The basic
algorithm was invented in 1992 and can be found, e.g., in
[3].
Given two independently acquired sets of 3D points,  (model set,
(model set,
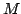 ) and
) and 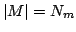 (data set,
(data set, 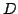 ) which correspond to a
single shape, we aim to find the transformation consisting of a
rotation
) which correspond to a
single shape, we aim to find the transformation consisting of a
rotation 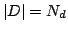 and a translation
and a translation 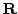 which minimizes the following
cost function:
which minimizes the following
cost function:
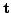 |
(1) |
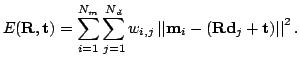 is assigned 1 if the
is assigned 1 if the  -th point of
-th point of  describes the same
point in space as the
describes the same
point in space as the  -th point of
-th point of  . Otherwise
. Otherwise 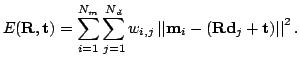 is
0. Two things have to be calculated: First, the corresponding points,
and second, the transformation (
is
0. Two things have to be calculated: First, the corresponding points,
and second, the transformation ( ,
,  ) that minimize
) that minimize
 on the base of the corresponding points. The ICP algorithm
calculates iteratively the point correspondences. In each iteration
step, the algorithm selects the closest points as correspondences and
calculates the transformation (
on the base of the corresponding points. The ICP algorithm
calculates iteratively the point correspondences. In each iteration
step, the algorithm selects the closest points as correspondences and
calculates the transformation (
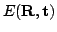 ) for minimizing equation
(
) for minimizing equation
(![[*]](file:/usr/share/latex2html/icons/crossref.png) ). The assumption is that in the last iteration step the
point correspondences are correct. Besl et al. prove that the method
terminates in a minimum [3]. However, this theorem does
not hold in our case, since we use a maximum tolerable distance
). The assumption is that in the last iteration step the
point correspondences are correct. Besl et al. prove that the method
terminates in a minimum [3]. However, this theorem does
not hold in our case, since we use a maximum tolerable distance
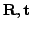 max for associating the scan data. Here
max for associating the scan data. Here
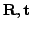 max is
set to 15 cm for the first 15 iterations and then this threshold is
lowered to 5 cm. Fig.
max is
set to 15 cm for the first 15 iterations and then this threshold is
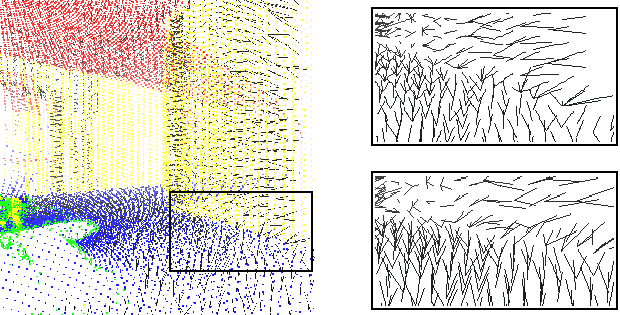
lowered to 5 cm. Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) (left) shows two 3D scans
aligned only according to the error-prone odometry-based pose
estimation. The point pairs are marked by a line.
(left) shows two 3D scans
aligned only according to the error-prone odometry-based pose
estimation. The point pairs are marked by a line.
Figure:
Point pairs for the ICP scan matching algorithm. The
left image show parts of two 3D scans and the closest point
pairs as black lines. The right images show the point pairs in
case of semantically based matching (top) whereas the bottom
part shows the distribution with closest points without taking
the semantic point type into account.
|
|
Subsections



Next: Computing the Optimal Rotation
Up: 3D Mapping with Semantic
Previous: Extracting Semantic Information
root
2005-05-03
 (model set,
(model set,
 (model set,
(model set,
![]() ) and
) and ![]() (data set,
(data set, ![]() ) which correspond to a
single shape, we aim to find the transformation consisting of a
rotation
) which correspond to a
single shape, we aim to find the transformation consisting of a
rotation ![]() and a translation
and a translation ![]() which minimizes the following
cost function:
which minimizes the following
cost function:
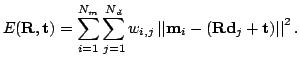 is assigned 1 if the
is assigned 1 if the  describes the same
point in space as the
describes the same
point in space as the 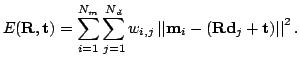 is
0. Two things have to be calculated: First, the corresponding points,
and second, the transformation (
is
0. Two things have to be calculated: First, the corresponding points,
and second, the transformation (