

Next: Semantic Scene Interpretation
Up: Automatic Model Refinement for
Previous: Matching Multiple 3D Scans
A common technique for plane extraction is the region growing
based approach, e.g., used by Hähnel et al.
(12). Starting from an initial mesh, neighbored
planar triangles are merged iteratively. The drawback of this
approach is the high computational demand. Alternatively the
approach of online surfaces detection based on line detection in
scan slices of a 3D scans (23) reduces the
computational requirements (23), but extending this
approach to multiple 3D scans leads to difficulties.
Another well known algorithm for feature extraction from data
sets is the RANSAC algorithm (1), used by Cantzler et
al. (6). RANSAC (Random Sample Consensus) is
a simple algorithm for robust fitting of models in the presence
of many data outliers. RANSAC first selects 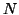 data items
randomly and uses them to estimate the parameters of the
plane. The next step computes the number of data points fitting
the model based on a user given tolerance. RANSAC accepts the
fit, if the computed number exceeds a certain limit. Otherwise
the algorithm iterates with other points (1).
Liu et al. proposes another technique for plane extraction from
range data. They use expectation maximization (EM) for generating a
surface model (15). Their algorithm adjusts the number
of planes and estimates the location and orientation, by
maximizing the expectation of a logarithmic likelihood
function. Plane parameters are efficiently calculated by reducing
the problem to a computation of eigenvalues by introducing
Lagrange multipliers. This approach is not inherently able to
determine the number of planes in the data set
(12).
Our algorithm is a mixture of the RANSAC and the ICP algorithm,
and provides fast plane extraction for a point cloud. No prior
meshing algorithms needs to be applied. A plane
data items
randomly and uses them to estimate the parameters of the
plane. The next step computes the number of data points fitting
the model based on a user given tolerance. RANSAC accepts the
fit, if the computed number exceeds a certain limit. Otherwise
the algorithm iterates with other points (1).
Liu et al. proposes another technique for plane extraction from
range data. They use expectation maximization (EM) for generating a
surface model (15). Their algorithm adjusts the number
of planes and estimates the location and orientation, by
maximizing the expectation of a logarithmic likelihood
function. Plane parameters are efficiently calculated by reducing
the problem to a computation of eigenvalues by introducing
Lagrange multipliers. This approach is not inherently able to
determine the number of planes in the data set
(12).
Our algorithm is a mixture of the RANSAC and the ICP algorithm,
and provides fast plane extraction for a point cloud. No prior
meshing algorithms needs to be applied. A plane 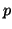 is defined by
three 3D points (
is defined by
three 3D points (
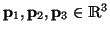 ) or by one 3D
point and the surface normal (
) or by one 3D
point and the surface normal (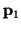 ,
, 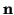 with
with
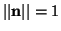 ,
,
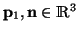 ). To detect a surface the algorithm
randomly selects a point and estimates a plane through two
neighbored data points. Now the data points
). To detect a surface the algorithm
randomly selects a point and estimates a plane through two
neighbored data points. Now the data points
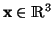 are calculated that fulfill:
are calculated that fulfill:
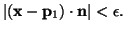 |
|
|
(2) |
If this set of points exceeds a limit, e.g., 50 points, an ICP
based optimization is started. All data points satisfying
eq. (2) form the model set 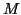 and are projected to
the plane to form the data set
and are projected to
the plane to form the data set 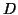 for each iteration of the ICP
algorithm. Minimizing the ICP error function (1) by
transforming the plane with this point-to-plane metric takes only
a few iterations. The time consuming search is replaced by direct
calculation of the closest point and the transformation (
for each iteration of the ICP
algorithm. Minimizing the ICP error function (1) by
transforming the plane with this point-to-plane metric takes only
a few iterations. The time consuming search is replaced by direct
calculation of the closest point and the transformation (
 ) is efficiently calculated (14). Given the best
fit, all plane points are marked and subtracted from the original
data set. The algorithm terminates after all points have been
tested according to eq. (2).
The extracted 3D planes are unbounded in size. Surfaces are
finally extracted from the points by mapping them onto the
planes. A quadtree based method generates the surfaces. Figure
4 shows an example with 12 extracted planes of a
single 3D scan containing 184576 range data points.
) is efficiently calculated (14). Given the best
fit, all plane points are marked and subtracted from the original
data set. The algorithm terminates after all points have been
tested according to eq. (2).
The extracted 3D planes are unbounded in size. Surfaces are
finally extracted from the points by mapping them onto the
planes. A quadtree based method generates the surfaces. Figure
4 shows an example with 12 extracted planes of a
single 3D scan containing 184576 range data points.


Next: Semantic Scene Interpretation
Up: Automatic Model Refinement for
Previous: Matching Multiple 3D Scans
root
2003-08-06