

Next: Model Refinement
Up: Automatic Model Refinement for
Previous: Feature Detection
The scene interpretation uses the features, i.e., planes found by
the algorithm described in the previous section. The background
for interpretation comprises generic architectural knowledge. A
model of an indoor scene is implemented as a semantic net based
on the idea of Grau et al. (11) and also used by
Cantzler et al. (6).
Nodes of a semantic net represent entities of the world /
model. The relationship between the entities are encoded using
different connections. Possible labels of the nodes are
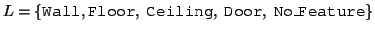 . The relationships
between the features are
. The relationships
between the features are
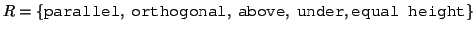 . The labels above and
under are relative to their plane and hence not
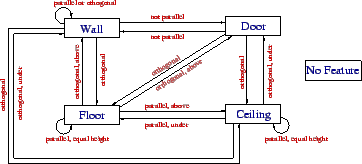
commutative. Figure 3 shows the entities and the
relation. The reader should notice that in our semantic net a
door is an open door. The semantic net can easily
be extended to more entities which have be accompanied by a more
sophisticated feature detection. This paper concentrates on plane
detection so that the semantic net is a subset of all indoor
environments.
. The labels above and
under are relative to their plane and hence not
commutative. Figure 3 shows the entities and the
relation. The reader should notice that in our semantic net a
door is an open door. The semantic net can easily
be extended to more entities which have be accompanied by a more
sophisticated feature detection. This paper concentrates on plane
detection so that the semantic net is a subset of all indoor
environments.
Figure 3:
Semantic net for scene interpretation.
 |
A depth first search (backtracking) is implemented to assign the
labels to the set of planes 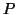 according to the constraints in
the semantic net. The search starts by assigning the first label
from
according to the constraints in
the semantic net. The search starts by assigning the first label
from 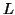 to the first plane. The second plane is labeled and
tested with the constraints given by the net. If all constraints
are satisfied the search continues with the next plane. Otherwise
backtracking starts with further labels. This process terminates
after the whole search tree is tested and all consistent
combinations are generated. A consistent labeling exists if each
plane is assigned with a label and the model graph is arc
consistent. From all consistent labelings our algorithm chooses
the labeling that maximizes
to the first plane. The second plane is labeled and
tested with the constraints given by the net. If all constraints
are satisfied the search continues with the next plane. Otherwise
backtracking starts with further labels. This process terminates
after the whole search tree is tested and all consistent
combinations are generated. A consistent labeling exists if each
plane is assigned with a label and the model graph is arc
consistent. From all consistent labelings our algorithm chooses
the labeling that maximizes
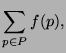 |
|
|
(3) |
where 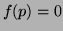 if plane
if plane 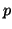 is assigned to No_Feature,
is assigned to No_Feature, 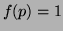 if the plane is assigned to Wall, Door, Floor or Ceiling. The
maximization of (3) ensures correct labelings
containing Floor, Ceiling and Walls with the minimal number of
No_Features and requires a complete tree search.
The computational expense is reduced by backtracking pruning and
reusing (caching) of constraint tests, e.g., the verification
that two planes are orthogonal. Especially the constraints
"under" and "above" require a distance computation with all
points of the plane. Figure 4 shows the
interpretation of extracted planes from a point cloud acquired in
the GMD Robobench, a standard office environment for the
evaluation of autonomous mobile robots. The plane labeled with
door is an slightly opened office door.
if the plane is assigned to Wall, Door, Floor or Ceiling. The
maximization of (3) ensures correct labelings
containing Floor, Ceiling and Walls with the minimal number of
No_Features and requires a complete tree search.
The computational expense is reduced by backtracking pruning and
reusing (caching) of constraint tests, e.g., the verification
that two planes are orthogonal. Especially the constraints
"under" and "above" require a distance computation with all
points of the plane. Figure 4 shows the
interpretation of extracted planes from a point cloud acquired in
the GMD Robobench, a standard office environment for the
evaluation of autonomous mobile robots. The plane labeled with
door is an slightly opened office door.
Figure 4:
Left: Point cloud. Middle and right: Extracted planes
and semantic interpretation.
 |


Next: Model Refinement
Up: Automatic Model Refinement for
Previous: Feature Detection
root
2003-08-06
