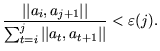


Next: Polygon-Generierung
Up: Software Module des AIS
Previous: Software Module des AIS
Der Servo wird direkt vom Echtzeitbetriebssystem RealTime-Linux
angesteuert. Ein Servomotor erwartet alle 20ms einen TTL-Impuls. Dabei
bestimmt die Länge des Impulses die Position des Servos (1ms = Links,
1.5ms = Mitte, 2ms = Rechts). Dies ist eine sehr zeitkritische
Aufgabe, da bereits eine Abweichung von 10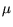 s zu einem Fehler von
1° führt. RealTime Linux hat eine durchschnittliche Latenz von 5
s zu einem Fehler von
1° führt. RealTime Linux hat eine durchschnittliche Latenz von 5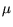 s
(PII-333). Somit kann die Rotation bis auf ein halbes Grad genau
realisiert werden.
s
(PII-333). Somit kann die Rotation bis auf ein halbes Grad genau
realisiert werden.
Während des Scans werden verschiedene Online-Algorithmen zur Linien-
und Flächenerkennung eingesetzt. Der erste Schritt der
Messdatenverarbeitung ist die Linienerkennung (vgl. Abbildungen
2.5, 2.6 und 3.7), die auf jedem
2D-Schnitt einzeln ausgeführt wird. Dabei kommen wahlweise zwei
Algorithmen zum Einsatz: Ein einfacher Matching-Algorithmus oder die
Hough-Transformation. Der Matching-Algorithmus betrachtet die Punkte
in der durch den Scanprozess bestimmten Reihenfolge. Die Messpunkte
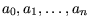 sind gegen den Uhrzeigersinn geordnet. Wenn die
Punkte
sind gegen den Uhrzeigersinn geordnet. Wenn die
Punkte
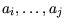 bereits auf einer Linie liegen, muss folgende
Bedingung erfüllt sein, damit auch der Punkt
bereits auf einer Linie liegen, muss folgende
Bedingung erfüllt sein, damit auch der Punkt 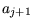 auf der Linie
liegt:
auf der Linie
liegt:
Dieser Test kann sehr schnell durchgeführt werden, die Qualität der
Linien ist jedoch wegen des Rauschens der Messdaten nicht optimal. Um
die negativen Effekte der Messabweichungen zu verringern,
wird der Linienerkenner nicht direkt auf die Messdaten, sondern auf so genannte
REDUZIERTE PUNKTE angewendet. Dicht beieinander liegende
Messpunkte werden gemittelt und zu einem Punkt zusammengefasst. Dies
dünnt die Werte aus und die Anzahl reduziert sich (vgl. Abbildung
2.5). Die Hough-Transformation (
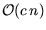 ,
, 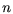 = Anzahl der
Scan-Punkte,
= Anzahl der
Scan-Punkte, 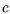 abhängig von der maximalen Entfernung) liefert
qualitativ bessere Linien, ist jedoch nur begrenzt als
Online-Algorithmus einsetzbar, da die Konstante
abhängig von der maximalen Entfernung) liefert
qualitativ bessere Linien, ist jedoch nur begrenzt als
Online-Algorithmus einsetzbar, da die Konstante 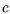 sehr groß
wird. Eine ausführliche Darstellung der Hough-Transformation ist in
[75] zu finden.
sehr groß
wird. Eine ausführliche Darstellung der Hough-Transformation ist in
[75] zu finden.
Abbildung 2.5:
Messpunkte, REDUZIERTE PUNKTE und erkannte Linien in einem Scanschnitt.
|
|
Anschließend findet die 3. Dimension Berücksichtigung. Aus den
detektierten Linien werden sukzessive Flächen gebaut. Dabei wird eine
Linie, bzw. die oberste Linie einer bereits vorhandenen Fläche, mit
einer neu erkannten Linie vereinigt, falls folgende Kriterien erfüllt
sind:
- Die Endpunkte der neuen Linien müssen in einer Epsilon-Umgebung der
Endpunkte von den bereits vorhandenen Linien liegen.
- Der Winkel zwischen den beiden Linien sollte einen gewissen
Schwellenwert nicht überschreiten.
- Die neu erkannte Linie muss in der Ebene der bereits vorhandenen Fläche
liegen.
Dieses sukzessive Vergrößern angewendet auf jede Scan-Ebene
der Flächen ist als Online-Algorithmus implementiert, wird also
während des Scanprozesses ausgeführt.
Abbildung 2.6:
Messpunkte und detektierte Linien.
|
|



Next: Polygon-Generierung
Up: Software Module des AIS
Previous: Software Module des AIS
Andreas Nüchter
2002-07-10
![]() s zu einem Fehler von
1° führt. RealTime Linux hat eine durchschnittliche Latenz von 5
s zu einem Fehler von
1° führt. RealTime Linux hat eine durchschnittliche Latenz von 5![]() s
(PII-333). Somit kann die Rotation bis auf ein halbes Grad genau
realisiert werden.
s
(PII-333). Somit kann die Rotation bis auf ein halbes Grad genau
realisiert werden.
![]() sind gegen den Uhrzeigersinn geordnet. Wenn die
Punkte
sind gegen den Uhrzeigersinn geordnet. Wenn die
Punkte
![]() bereits auf einer Linie liegen, muss folgende
Bedingung erfüllt sein, damit auch der Punkt
bereits auf einer Linie liegen, muss folgende
Bedingung erfüllt sein, damit auch der Punkt ![]() auf der Linie
liegt:
auf der Linie
liegt: