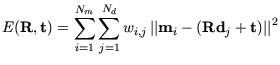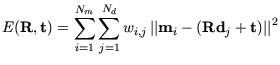


Next: Rotationsbestimmung
Up: Berechnung der optimalen Rotation
Previous: Berechnung der optimalen Rotation
Die zu minimierende Fehlerfunktion
Nach dem Einsetzen der Gleichungen (3.11), (3.12),
(3.13) und (3.14) in die Fehlerfunktion
ergibt sich
Um die obige Summe zu minimieren, müssen alle Terme minimiert werden.
Der zweite Term (A.16) ist Null, da sich die Werte auf den
Schwerpunkt beziehen. Der dritte Teil (A.17) hat für
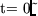 bzw.
bzw.
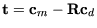 ein
Minimum. Folglich bleibt der erste Teil (A.15) übrig und
die neue Fehlerfunktion lautet:
ein
Minimum. Folglich bleibt der erste Teil (A.15) übrig und
die neue Fehlerfunktion lautet:
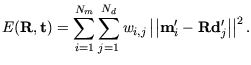 |
|
|
(7.18) |



Next: Rotationsbestimmung
Up: Berechnung der optimalen Rotation
Previous: Berechnung der optimalen Rotation
Andreas Nüchter
2002-07-10