|
Im folgenden werden Strategien zur Interpretation der Scan-Ergebnisse erläutert, insbesondere zur Segmentierung der Bildelemente in einzelne, größere Objekte. Im Gegensatz zu dem vorherigen Kapitel sind dies Algorithmen, die aufgrund ihrer Komplexität offline durchzuführen sind.
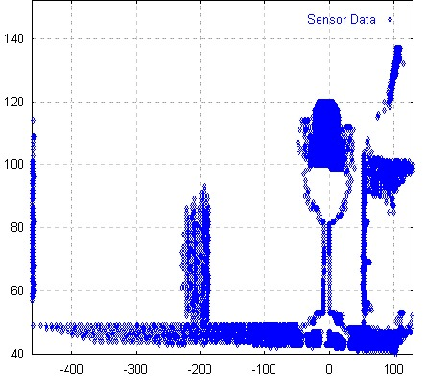
Der Scanner liefert die Daten der Umgebung in einzelnen
![]() -Schnitten durch den Raum. Ein Scan läßt sich also als
eine Art ,,Draufsicht`` auf den Raum von oben aus sehen, mit
steigender Scannummer steigt insbesondere die Höhe des Schnittes.
-Schnitten durch den Raum. Ein Scan läßt sich also als
eine Art ,,Draufsicht`` auf den Raum von oben aus sehen, mit
steigender Scannummer steigt insbesondere die Höhe des Schnittes.
Da diese Ansicht jedoch ausgesprochen unintuitiv ist, bestand der
erste Versuch nun darin, die Daten eines kompletten 3D-Scan in
![]() -Richtung zu projizieren, um auf diese Weise eine Art Frontalansicht zu
erhalten. Dies bedeutet, daß - vom Betrachter aus gesehen - mit
wachsender Scannummer die
-Richtung zu projizieren, um auf diese Weise eine Art Frontalansicht zu
erhalten. Dies bedeutet, daß - vom Betrachter aus gesehen - mit
wachsender Scannummer die ![]() -Ebene weiter nach hinten
wandert.4.1
-Ebene weiter nach hinten
wandert.4.1
Es folgen nun - sofern nicht anders erwähnt - zunächst einmal Algorithmen, die auf diesen 2D-Projektionen arbeiten. Später jedoch wird ein Wechsel zu Verfahren stattfinden, die direkt in dem 3D-Bild arbeiten.
Der naheliegendste Ansatz bestand in der Anwendung eines
Gradientenfilters [Hab91,Shi87] auf das Bild: Jeder Bildpunkt
![]() mit
Grauwert
mit
Grauwert
![]() bekommt den neuen Grauwert
bekommt den neuen Grauwert
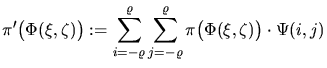 |
(4.1) |
Dabei ist die Filter-Matrix ![]() je nach zu verwendetem Filtern
(
je nach zu verwendetem Filtern
(![]() -Gradient,
-Gradient, ![]() -Gradient) zu wählen als:
-Gradient) zu wählen als:
![$\displaystyle \substack{\left[\begin{array}{*{3}{r}} -1 & -1 & -1 \\ 0 & 0 & 0...
... -1 & 0 & 1 \end{array}\right]\\ [1ex] \text{\footnotesize ($Y$--Gradient)}} $](img167.gif)
Ein sehr viel besseres Ergebnis lieferte ein Laplace-Filter mit folgender Filtermaske (
![]() ):
):
![$\displaystyle \Phi := \left[\begin{array}{*{3}{r}} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{array}\right] $](img169.gif)
Dieser Filter erkennt auch nichtlineare Krümmungen im Grauwertverlauf des Bildes unabhängig von ihrer Richtung (siehe Abbildung 4.3). Da er im allgemeinen auf Rauschen empfindlich reagiert, wird gewöhnlich eine Glättung des Bildes vorgeschaltet, was jedoch bei Tests auf unseren Daten keinen positiven Erfolg brachte. Das mag daran liegen, daß im allgemeinen Fall von Grauwertbildern ausgegangen wird, hier jedoch binäre Bilddaten vorliegen.
Mit Hilfe des im Abschnitt 3.2.1 beschriebenen Linienerkennungs-Algorithmus wird nun das Kantenbild vektorisiert, d.h. es wird in eine Anzahl von Linien transformiert. Diese Linien, bestehend aus Anfangs- und Endpunkt, ermöglichen nun die weitere Untersuchung des Scans wie die Segmentierung und anschließende Erkennung von Objekten.
Ein mögliches Ergebnis der Vektorisierung ist in Abbildung 4.4 zu betrachten. Jedoch arbeitet der verwendete Linienerkennungs-Algorithmus naturgemäß unter Verwendung einer Vielzahl von heuristischen Parametern, so daß an dieser Stelle eine Optimierung dieser Parameter aufgrund einer größeren Anzahl von Bildvorlagen notwendig ist. Dabei ist die ,,optimale`` Einstellung allerdings nicht eindeutig, je nach Zielsetzung der Vektorisierung kann eine Änderung einiger Einstellungen vonnöten sein. So ist es hier beispielsweise sinnvoll, von einer allzu perfekten Nachbildung des Ausgangsbildes abzusehen (es ist durchaus möglich, jede Ecke und Kante durch eine eigene Linie beschreiben zu lassen), da solch ein Ergebnis zwar optisch sehr realistisch aussieht, jedoch beispielsweise eine sinnvolle Flächenerkennung als nahezu unmöglich gestaltet.
Es sei jedoch angemerkt, daß dieses Vorgehen trotz der damit einhergehenden Informationsreduzierung durchaus seine Berechtigung hat. Schließlich soll es nicht zur kompletten Interpretation der Szene dienen, sondern lediglich das Erkennen eines Objektes erleichtern, nachdem die Szene in einzelne Objekte/Cluster segmentiert worden ist. Eingedenk der bisher noch schwer zu bewertenden Ergebnisse der im folgenden skizzierte Algorithmen ist es durchaus möglich, daß der Ansatz der Koordinatenprojektion wieder als additives Vorgehen Verwendung findet, um die bereits implementierten Algorithmen bei der Aufgabe der Objekterkennung zu unterstützen.
Von dem ersten Versuch weitgehend abstrahiert, besteht die
aktuelle Umsetzung schematisch gesehen aus folgenden Schritten:
Dieses Vorgehen wird im folgenden näher beschrieben.
Nähere Informationen über den genauen Ablauf und implementationsspezifische Details sind in Abschnitt 5,
Seite ![[*]](cross_ref_motif.gif) zu finden.
zu finden.
Ziel eines solchen Objektes ist es nun, hinreichend nahe beieinander liegende Elemente - dies sind primär kleinere Flächen und Anhäufungen von singulären Linien, jedoch können auch Punkte/Punktwolken durchaus von Interesse sein - zu clustern. Diese Cluster werden mit einer Bounding Box umgeben und im folgenden als ein einzelnes Objekt betrachtet; jedoch bleiben Referenzen auf diese das Objekt bestimmenden Elemente weiterhin gespeichert, um spätere direkte Zugriffe zu ermöglichen.
Der Objektsegmentierung liegt die Idee zugrunde, daß die oben beschriebenen, noch verbleibenden Elemente sich im allgemeinen zu sinnvoll segmentierbaren Wolken gruppieren, die ein Clustering ermöglicht. Sei beispielsweise ein Stuhl gegeben. Dieser wird im 3D-Scan zwar ein recht klares Bild aus Einzel-Punkten ergeben, jedoch schon die Linienerkennung wird bestenfalls viele kurze, gegeneinander verdrehte Linien finden, welche unmöglich zu einer (großen) Fläche segmentiert werden können (was im Übrigen trivialerweise auch nicht erwünscht wäre).
Wenn jedoch nun ein Element dieses Stuhles, beispielsweise eine kleine Fläche, die die Rückenlehne approximiert, oder auch nur eine einzelne Linie, als Ausgangspunkt genommen wird und davon ausgehend alle Elemente gruppiert werden, welche sich in hinreichend enger Nachbarschaft zu diesem Ausgangspunkt befinden, so werden im Idealfall auf diese Weise alle Elemente, die den Stuhl bestimmen, zu einem Objekt geclustert.
Zum besseren Verständnis sei noch erwähnt, daß bei oben beschriebenem Szenario der ,,Ausgangspunkt`` selber schon als Objekt betrachtet wird, welches es im folgenden gilt zu vergrößern, zu expandieren. Durch das Aufnehmen weiterer Elemente, die sich hinreichend nahe befinden, ,,wächst`` das Objekt, es vergrößert sich in seinen Ausmaßen. Auf diesen Sachverhalt wird jedoch in Abschnitt 4.2.1 noch näher eingegangen.
Je nach Einstellung zugehöriger heuristischer Parameter werden dabei offensichtlich nahe beieinander stehende Objekte zu einem einzigen verschmolzen. Dies ist zur Erkennung von Hindernissen, denen ein Roboter auszuweichen hat, gerade erwünscht. (Für dicht möblierte Räume kann sogar nur eine einzige Bounding Box existieren.)
Resultat: Der Algorithmus liefert eine Aufteilung der Scene in Objekte dergestalt, daß Akkumulationen von Punkten, Linien und/oder Flächen zu einzelnen Objekten zusammengefaßt und dabei von einer Bounding Box umschlossen werden. Diese Bounding Box stellt nicht nur einen wichtigen Schritt zur Objekterkennung dar. Vielmehr ermöglicht sie ferner die effiziente Navigation um dreidimensionale Hindernisse herum, deren exakte Form zu diesem Zweck nicht notwendig ist [Sur01].