In diesem Kapitel wird die Umsetzung der zeitkritischen Prozesse beschrieben. Dies sind zum einen das unterliegende Betriebsystem RT-Linux, zum anderen die implementierten Online-Algorithmen wie die Linienerkennung und die Flächensegmentierung.
Real-Time Linux ist ein Betriebssystem, bei dem ein kleiner Echtzeitkernel und der Linux Kernel nebeneinander existieren. Es soll erreicht werden, daß die hochentwickelten Aufgaben eines Standardbetriebssystems für Anwendungen zur Verfügung gestellt werden, ohne auf Echtzeitaufgaben mit definierten, kleinen Latenzen zu verzichten. Bisher waren Echtzeitbetriebssysteme kleine, einfache Programme, die nur wenige Bibliotheken dem Anwender zur Verfügung gestellt haben.
Mittlerweile ist es aber notwendig geworden, daß auch Echtzeitbetriebssysteme umfangreiche Netzwerk-Bibliotheken, Graphische Benutzeroberflächen, Datei- und Datenmanipulationsroutinen zur Verfügung stellen müssen. Eine Möglichkeit ist es, diese Features zu den existierenden Echtzeitbetriebssystemen hinzuzufügen. Dies wurde beispielsweise bei den Betriebssystemen VXworks und QNX gemacht. Eine andere Herangehensweise ist, einen bestehenden Betriebssystemkernel dahingehend zu modifizieren, daß dieser Echtzeitaufgaben bewältigt. Ein solcher Ansatz wird von den Entwicklern von RT-IX (Modcomp) verfolgt. RT-IX ist eine UNIX System V Implementation, die auch harte Echtzeitaufgaben bewältigen kann [Kuh98].
Real-Time Linux basiert auf einer dritten Herangehensweise. Ein kleiner Echtzeitkernel läßt ein Nicht-Echtzeitbetriebssystem als einen Prozeß mit niedrigster Priorität laufen. Dabei wird eine virtuelle Maschine für das eingebettete Betriebssystem benutzt.
Real-Time Linux behandelt alle Interrupts zuerst und gibt diese dann an den Linux Betriebssystem-Prozeß weiter, wenn diese Ereignisse nicht von Echtzeit-Prozessen behandelt werden. Durch einen solchen Aufbau sind minimale Änderungen am Linux Kernel nötig, da der Interrupt Handler auf den Echtzeitkernel abgestimmt werden muß. Der Real-Time Linux Kernel selbst ist ein ladbares Modul und kann bei Bedarf eingefügt und entfernt werden. Dieser Kernel stellt hauptsächlich die Schicht zwischen dem Linux Kernel und der Hardware-Interruptebene dar.
Real-Time Linux mutet anfänglich sehr spartanisch an, denn es liegt der Gedanke zugrunde, daß die Prinzipien von harten Real-Time Anwendungen in der Regel nicht vereinbar sind mit komplexer Synchronisation, dynamischer Resourcenverwaltung und allem anderen, was zeitliche Mehrkosten verursacht. Daher werden in der Standardkonfiguration nur sehr einfache Konstrukte zur Implementierung von Prozessen zur Verfügung gestellt, beispielsweise ein einfacher fixed priority scheduler, nur statisch allozierter Speicher und und kein Schutz des Adreßraums. Dennoch kann man mit den gegebenen Mitteln sehr effizient arbeiten, da alle Nicht-Echtzeitkomponenten unter Linux laufen und somit dortige Bibliotheken benutzen können.
Real-Time Programme bzw. Prozesse werden als ladbare Module eingebunden, was das Echtzeitbetriebssystem erweiterbar und einfach zu modifizieren macht. Die Programme werden mit den Standard-Linux-Werkzeugen erzeugt (GNU C compiler). Oftmals übernehmen andere, Nicht-Real-Time Programme die weitere Datenverarbeitung. Da Real-Time Linux keinerlei Mechanismen zum Schutz gegen Überladung der Hardware besitzt, ist es möglich, daß die Real-Time Prozesse die CPU blockieren. In diesem Fall bekommt der Linux Kernel nicht die Chance, eine Zeitscheibe zu bekommen, da er die niedrigste Priorität hat.
Da Real-Time Linux OPENSOURCE ist und da die Module von Real-Time Linux ladbar und damit jederzeit austauschbar, sind, fand eine breite Entwicklung von Zusatzmodulen statt. Als Zusatzmodule stehen zur Zeit alternative Scheduler (z.B. rate-monotonic scheduler), ein Semaphore Modul, IPCs (interprocess communication Mechanismen) und etliche Real-Time device driver zur Verfügung.
Real-Time und Linux-User Prozesse kommunizieren über lock-freie Queues (FIFOs) und shared memory. Anwendungsprogrammierern stellen sich die FIFOs als standard character devices dar, auf die mittels POSIX read/write/open/ioctl zugegriffen wird.
Es hat sich gezeigt, daß Real-Time Linux den Anforderungen eines
Echtzeitbetriebssystems sehr nahekommt. Die Worst-Case interrupt
latency auf einem 486/33MHz PC liegt unter 30![]() s (
s (
![]() s)
und somit nahe dem Hardwarelimit [RTL98].
s)
und somit nahe dem Hardwarelimit [RTL98].
Von Real-Time Linux gibt es verschiedene Versionen. Etliche kommerzielle Hersteller bieten ihre Versionen von dem Betriebssystem Real-Time Linux an. Wir beziehen uns im folgenden auf die frei erhältliche Version dieses Betriebssystems, siehe [ URLFsm].
Real-Time Linux gibt es bereits in der 3. Version. Mit der ersten Version wurde das Konzept implementiert und getestet. In Version 2 wurden etliche Features und die ganze API überarbeitet sowie mit dem Betriebssystem POSIX konform gemacht. Es wird Real-Time Linux Version 2.2a verwendet, die auf dem letzten stabil laufendem Linux Kernel basiert (Kernel Version 2.2.14) (Stand: Juni 2000). Die neue Version 3 basiert auf den noch nicht freigegebenen Kernel der 2.4er Serie.
Die Tabelle 3.1 zeigt die Real-Time Linux Versionen vs. den Linux Kernel Versionen.
Zur Installation benötigt man nur ein lauffähiges Linux. Man lädt sich einen frischen, d.h. ungepatchten Kernel und den Real-Time Linux Patch. Alternativ dazu kann man sich auch die vor-gepatchten Kernelquellen besorgen. Danach folge man den Anweisungen der Installations-Dateien.
Problematisch ist die Installation, wenn man andere Kernelversionen als die zu Real-Time Linux gehörenden verwenden möchte. Der Real-Time Patch läßt sich i.A. nur auf die Kernelversion anwenden, für die er geschrieben wurde. Für den Fall, daß andere Patches angewendet werden müssen, sollte man diese auf den Real-Time Quellcode anwenden. So ist es möglich, ein Real-Time fähiges Betriebssystem und Unterstützung mit USB (Universal Serial Bus) verbinden zu können.
Im folgenden sind die wichtigsten in der Scanner-Software verwendeten Real-Time Interfacefunktionen vorgestellt. Dabei wird die neue POSIX-konforme API V2 verwendet.
Die Aufrufe zur Prozeß-Verwaltung sind in der ab Version 2 dem Standard pthread angeglichen wurden. Für einen Real-Time-Prozeß steht folgende Struktur zur Verfügung.
struct rtl_thread_struct {
int *stack; /* hardcoded */
int uses_fp;
enum rtl_task_states state;
int *stack_bottom;
rtl_sched_param sched_param;
struct rtl_thread_struct *next;
RTL_FPU_CONTEXT fpu_regs;
int cpu;
hrtime_t resume_time;
hrtime_t period;
void *retval;
int pending_signals;
struct tq_struct free_task;
void *user[4];
int errno_val;
int pad [64];
};
typedef struct rtl_thread_struct RTL_THREAD_STRUCT;
typedef RTL_THREAD_STRUCT *pthread_t;
Es genügt daher, einen Thread wie folgt zu definieren.
pthread_t REALTIME_TASK;Eine Funktion (Prozeß) kann nun diesem Thread zugeordnet und gestartet werden:
int pthread_create(pthread_t *thread,
pthread_attr_t *attr,
void *(*start_routine)(void *),
(void *arg));
Nun muß der Prozeß periodisch gemacht werden. Dies geschieht mittels
folgender nicht-posix konformer (erkennbar an dem Postfix ,, _np``) Funktion
int pthread_make_periodic_np(pthread_t thread,
hrtime_t start_time,
hrtime_t period);
Innerhalb des Prozesses lassen sich die Parameter des Threads (wie
beispielsweise die Periode REALTIME_TASK->period) beeinflussen.
Der Prozeß läßt sich bis zu dieser Periode mittels der Funktion
int pthread_wait_np(void);explizit schlafen legen, die Steuerung wird an andere Prozesse zurückgeben. Prozesse mit der Priorität 1 haben die höchste Priorität, der normale Linuxkernel wird mit der niedrigsten betrieben.
Für Zeiten in Real-Time Linux wird die Datenstruktur hrtime_t
verwendet. Dies ist ein 64-Bit Integer. Die aktuelle Auflösung der
Zeit (in Prozessorticks) durch diese Variable ist
hardwareabhängig3.1, es wird aber garantiert, daß die Auflösungsgenauigkeit
unter 1![]() s (Mikrosekunde) liegt. Das Symbol HRTIME_INFINITY
repräsentiert den maximalen Wert und wird niemals erreicht. Das Symbol
HRTICKS_PER_SEC ist definiert als die Ticks pro Sekunde. Die
Funktion
s (Mikrosekunde) liegt. Das Symbol HRTIME_INFINITY
repräsentiert den maximalen Wert und wird niemals erreicht. Das Symbol
HRTICKS_PER_SEC ist definiert als die Ticks pro Sekunde. Die
Funktion
hrtime_t gethrtime(void);liefert die aktuelle Zeit.
Für Linux-Prozesse stehen die Real-Time FIFOs als character devices /dev/rtf0, /dev/rtf1 etc. zur Verfügung. Der Real-Time Prozeß muß die FIFOs explizit erzeugen und ihnen eine Größe geben. Dies geschieht mit der Funktion
int rtf_create(unsigned int fifo, int size);Innerhalb der Real-Time Applikation kann mit den Funktionen
int rtf_put(unsigned int fifo, char *buf, int count); int rtf_get(unsigned int fifo, char *buf, int count);auf die FIFOs zugegriffen werden. Eine wichtige Funktion ist der Handler, der immer dann aufgerufen wird, wenn eine Linux-User Programm auf einen FIFO zugreift. Ein solcher Handler wird mit folgender Funktion mit dem FIFO verbunden:
int rtf_create_handler(unsigned int fifo,
int (* handler)(unsigned int fifo)
);
Servomotoren werden üblicherweise im Modellbau eingesetzt. Handelsübliche Servos haben einen nominalen Winkelbereich von 90 Grad und erzeugen Drehmomente bis zu 150Ncm. Ein Servo verfügt über 3 Anschlußleitungen: Betriebsspannung, Masse und Steuersignal. Alle 20 Millisekunden erwartet der Servo als Steuersignal einen TTL-kompatiblen Impuls von 1 bis 2 Millisekunden Länge. Die Länge des Impulses bestimmt die Stellung des Servos, d.h. 1ms = links, 1.5ms = mitte, 2ms = rechts (vgl. Abbildung 3.1).
Genauigkeit der Servoansteuerung:
Um den Servo genau zu positionieren, muß die Länge des Signals
exakt eingehalten werden. Eine Abweichung von 10![]() s
entspricht ungefähr einer Abweichung von einem Grad. Messungen
an unserer eingesetzten Testmaschine (PII, 333MHz) haben ergeben, daß
man mit einer maximalen Latenz von 12
s
entspricht ungefähr einer Abweichung von einem Grad. Messungen
an unserer eingesetzten Testmaschine (PII, 333MHz) haben ergeben, daß
man mit einer maximalen Latenz von 12![]() rechnen muß. Die
durchschnittlichen Abweichung ist 5
rechnen muß. Die
durchschnittlichen Abweichung ist 5![]() und daher die Auflösung des
Servos 0.5 Grad. Damit ergeben sich - unter variablen Punktauflösungen des Scanners -
Auflösungen, die in Tabelle 3.2 dargestellt sind.
und daher die Auflösung des
Servos 0.5 Grad. Damit ergeben sich - unter variablen Punktauflösungen des Scanners -
Auflösungen, die in Tabelle 3.2 dargestellt sind.
Folgende Skizze veranschaulicht den einfachen Anschluß eines Servomotors an die paralleler Schnittstelle.
Das Verfahren zur Servoansteuerung läßt sich auf bis zu 12 Servos pro parallele Schnittstelle einfach erweitern.
Das Real-Time Modul steuert einen Servo an. Der periodische Prozeß in diesem Modul besteht im wesentlichen aus einer Schleife, die endlos durchlaufen wird. Als erstes wird die Zeit in Prozessorticks berechnet und überprüft, ob der Prozeß zu früh ausgeführt wird (early scheduling). Wenn die 20 ms erreicht sind, wird an der Leitung der parallelen Schnittstelle das TTL-Signal angelegt. Danach legt sich der Prozeß eine Zeit lang schlafen. Diese Zeit bestimmt die Stellung des Servos. Anschließend wird das Signal wieder gelöscht und die Kontrolle bis zum nächsten Durchgang an andere Prozesse abgegeben. Damit läßt sich bereits eine Stepper-Funktion realisieren.
Das Modul ist auch in der Lage, den Motor kontinuierlich zu drehen und nach erfolgter Drehung dem Anwendungsprogramm dies mitzuteilen. Zur Kommunikation werden 2 Real-Time FIFOs benutzt.
Durch den ersten FIFO ( /dev/rtf0) teilt das Anwendungsprogramm über folgendes Telegramm die Anweisungen mit:
struct msg_struct{
char option;
hrtime_t data1;
hrtime_t data2;
hrtime_t time;
};
Ist das übermittelte Zeichen ein N, so wird der Servo angewiesen,
die in data1 übermittelte Zeit (in Prozessorticks)
als Highimpuls auszugeben.
Der zweite FIFO ( /dev/rtf1) wird dazu benutzt, um dem Anwendungsprogramm das Ende einer Drehung mitzuteilen. Es wird nach Beenden der Drehung immer ein D in den FIFO geschrieben. Mittels non-blocking Fileoperationen kann das Anwendungsprogramm diesen Status kontinuierlich abfragen.
Die bisherigen Definitionen beziehen sich auf einen zweidimensionalen Scan, wie er von dem Laserscanner direkt übermittelt wird. Im folgenden nun die Überleitung zum Dreidimensionalen.
coord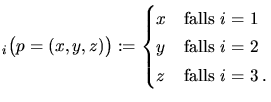 |
(3.1) |
| (3.2) |
Der erste Schritt der Meßdatenverarbeitung ist die Linienerkennung. Sie dient in erster Linie zur Datenreduktion für die nachfolgenden Schritte der Segmentierung und Objekterkennung. Linenerkenner auf 2D Laserscannerdaten werden schon recht erfolgreich in herkömmlichen Anwendungen zur Navigation eingesetzt [Arr96]. Die dort eingesetzten Linienerkenner sind speziell für Laserscanner geeignet.
Wir haben zwei Linienerkenner implementiert. Der erste Algorithmus von
Surmann und Liang [Pau98] ist ein einfacher Online-Algorithmus zum Detektieren
von Linien mit der Zeitkomplexität ![]() . Der zweite Linienerkenner
ist die aus der Bildverarbeitung bekannte Houghtransformation [Hab91]. Die
Houghtransformation ist recht gut für unsere Zwecke geeignet, da sie
auf einem schwarz/weiß Bild arbeitet. Somit sind die Scan-Punkte die
einzigen Bildpunkte. Dadurch ist die Houghtransformation immer noch
recht schnell, mit der Zeitkomplexität
. Der zweite Linienerkenner
ist die aus der Bildverarbeitung bekannte Houghtransformation [Hab91]. Die
Houghtransformation ist recht gut für unsere Zwecke geeignet, da sie
auf einem schwarz/weiß Bild arbeitet. Somit sind die Scan-Punkte die
einzigen Bildpunkte. Dadurch ist die Houghtransformation immer noch
recht schnell, mit der Zeitkomplexität
![]() , obwohl die Konstante wegen der großen
Scanreichweite recht groß werden kann. Desweiteren liefert die Houghtransformation
nicht nur die einzelnen Liniensegmente, sondern ebenfalls eine allgemeine
Geradengleichung der Form
, obwohl die Konstante wegen der großen
Scanreichweite recht groß werden kann. Desweiteren liefert die Houghtransformation
nicht nur die einzelnen Liniensegmente, sondern ebenfalls eine allgemeine
Geradengleichung der Form
![]() . Diese Geradengleichung entspricht einer
Ausgleichsgerade, die mehrere unterbrochene Liniensegmente verbindet.
Derartige Liniensegmente treten beispielsweise an Wänden auf, die durch Nischen,
Vorsprünge oder Türen unterbrochen sind.
. Diese Geradengleichung entspricht einer
Ausgleichsgerade, die mehrere unterbrochene Liniensegmente verbindet.
Derartige Liniensegmente treten beispielsweise an Wänden auf, die durch Nischen,
Vorsprünge oder Türen unterbrochen sind.
Der hier vorgestellte Linienerkenner wurde von Surmann und Liang speziell für 2D-Laserscanner entwickelt. Er kommt bei Robotern, die lediglich über 2D-Scanner zur Hindernisdedektierung verfügen, zum Einsatz. Der größte Vorteil dieses Verfahrens ist die Geschwindigkeit, denn dieser einfache Linienerkenner ist in der Praxis noch deutlich performanter als die ohnehin schon schnelle Houghtransformation.
Der Linienerkenner funktioniert in zwei Schritten,
Die Abbildung 3.3 zeigt einen 2D-Scan, Abbildung 3.4 die dazugehörigen reduzierte Datenmenge. Im Beispiel wurde mit einer stepDistance von 6 gearbeitet, d.h. alle Punkte in einem Radius von 6 cm werden zu einem einzelnen Punkt (ihrem Mittelpunkt) zusammengefaßt. Die 250 Meßwerte konnten damit auf 90 reduziert werden.
Der Linienerkenner geht sukzessive alle verbliebenen Punkte
durch,um Punkte zu Linien zusammenzufassen. Seien
![]() die Punkte. Weiterhin sei bereits bekannt, daß
die Punkte. Weiterhin sei bereits bekannt, daß
![]() auf einer Linien liegen. Nun betrachtet der
Algorithmus den Punkt
auf einer Linien liegen. Nun betrachtet der
Algorithmus den Punkt ![]() . Es werden folgende Werte berechnet:
. Es werden folgende Werte berechnet:
| distance | |||
| sum | 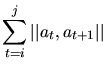 |
||
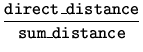 |
|||
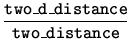 |
Die Linie
![]() wird nun um den Punkt
wird nun um den Punkt ![]() erweitert, wenn
alle der folgenden Bedingungen erfüllt sind:
erweitert, wenn
alle der folgenden Bedingungen erfüllt sind:
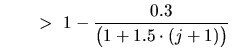
Wie man leicht sieht, wird mit ratio und ratio2 die Linienerkennung kontrolliert. Die 3. Ungleichung drückt aus, inwieweit Linien ohne vorliegende Meßpunkte extrapoliert werden. Die in den Ungleichungen auftretenden Konstanten wurden von uns empirisch bestimmt.
Abbildung 3.5 zeigt das Resultat des Linienerkenners auf den Meßpunkten aus Abbildung 3.4 (eingezeichnet in die Originaldaten). Ein Vergleich der beiden Abbildungen zeigt, daß alle Punkte, die nach dem Reduzieren übrig geblieben sind, auch Linien zugeordnet werden konnten.
Die Houghtransformation dient zum Erkennen von geometrischen
zweidimensionalen Objekten [McL98, URLHou].
Dazu wird eine
![]() -Parametrisierung des
Linienraums benutzt, wobei
-Parametrisierung des
Linienraums benutzt, wobei ![]() der Winkel des Normals zu der
Linie ist und
der Winkel des Normals zu der
Linie ist und ![]() die Länge des Normals, also der Abstand des
Punktes zum Ursprung des Bildes.
die Länge des Normals, also der Abstand des
Punktes zum Ursprung des Bildes.
Alle Punkte einer Linie erfüllen durch diese Parametrisierung die Gleichung
| (3.3) |
Ein Beispiel soll das Verfahren demonstrieren: Gegeben seien
vier Punkte (vgl. Abbildung 3.7): ![]() ,
, ![]() ,
,
![]() und
und ![]() . Wie man leicht sieht, liegen drei der vier
Punkte auf einer Geraden. Diese drei Punkte überlagern sich im
. Wie man leicht sieht, liegen drei der vier
Punkte auf einer Geraden. Diese drei Punkte überlagern sich im
![]() )-Raums konstruktiv und bilden im Histogramm dann ein
Maximum.
)-Raums konstruktiv und bilden im Histogramm dann ein
Maximum.
Diese Transformation wird für alle Punkte des Scans berechnet und
das Ergebnis in einem Histogramm aufsummiert. Dabei wird sowohl der
Winkel ![]() als auch
als auch
![]() diskretisiert [ URLHou].
diskretisiert [ URLHou].
for (i=0; i < nr_pts; i++) {
for (j=0; j < resolution; j++) {
// theta in [-PI/2,PI/2)
// Die Winkel theta sind in einem Array hinterlegt
rho = cos_theta[j] * (double) x[i] + sin_theta[j] *
(double) y[i];
k = (int) ((resolution) * (rho / (2.0 * max_rho_d) +
0.5));
histogram[j][k]++;
}
}
Danach wird im Histogramm das globalen Maximum bestimmt. Damit
errechnet man eine Geradengleichung und markiert alle zu dieser
Geraden gehörigen Punkte. Gleichzeitig werden alle Linien,
d.h. Geradensegmente als Ausgabe für die Houghtransformation,
bestimmt. Viele Parameter bestimmen die Güte der aus den Geraden
extrahierten Linien und wurden dahingehend angepaßt, daß möglichst
korrekt im nahen Sensorbereich erkannt wird. Anschließend werden die
Punkte, die zu einer Gerade gehören, von dem Histogramm
abgezogen. Dabei wird nicht nur das Maximum des Histogramms entfernt,
sondern auch alle Punkte, die zu der geraden beigetragen haben. Damit
senkt sich das Gesamtniveau des Histogramms also ab.
Dieser Prozeß wird iteriert, d.h. die Houghtransformation wird erneut gestartet mit den verbliebenen Punkten. Es wird solange iteriert, bis entweder alle Punkte in Geraden aufgegangen sind (hierbei werden einzelne Punkte als Ein-Punkt-Geraden erkannt), oder nach der 100sten Iteration abgebrochen wird.
Abbildung 3.8 stellt das zweidimensionale Histogramm dar und veranschaulicht die Entfernung von Geraden.
Bemerkung:
Die Houghtransformation liefert Geradengleichungen. Die hier vorgestellte Arbeit
benutzt zur Zeit nur die Linien-, d.h. Strecken-Information.
Die Houghtransformation jedoch liefert insbesondere Geradengleichungen,
welche die Möglichkeit bieten, aufgrund von Hintergrundwissen über die eingescannte
Szene verdeckte Linien zu propagieren. Wände lassen sich somit extrapolieren, was für Anwendungen in
der Robotik sehr sinnvoll ist.
Zum Abschluß geben wir zwei Beispiele. Abbildung 3.9 zeigt die mittels der Hough-Transformation
erkannten Linien zu den in den Abbildungen 3.8 dargestellten Histogrammen.
Abbildung 3.10 zeigt den gleichen 2D-Scan wie Abbildung
3.3 und ist hier als direkter Vergleich zu dem einfachen Linienerkenner angegeben.
Die beim Einscannen gelieferten Daten - die Punkte eines Scans -
müssen nun noch in das kartesische Koordinatensystem
![]() eines 3D-Scans umgerechnet werden. Die Scan-Punkte eines Scans sind
gegeben durch
eines 3D-Scans umgerechnet werden. Die Scan-Punkte eines Scans sind
gegeben durch ![]() Koordinaten und den aktuellen Neigungswinkel
des Scanners,
Koordinaten und den aktuellen Neigungswinkel
des Scanners, ![]() .
.
Die ![]() -Koordinaten werden aus den Meßwerten (
-Koordinaten werden aus den Meßwerten (![]() )
berechnet (vgl. Abbildung 3.11) durch
)
berechnet (vgl. Abbildung 3.11) durch
| (3.4) | |||
| (3.5) | |||
| (3.6) |
Bei der Texturberechnung wird jedem Punkt eindeutig ein Punkt auf dem Foto, beziehungweise auf dem aus mehreren Fotos zusammengesetzten Bild, zugeordnet. Als Textur-Koordinaten werden im folgenden die zu einem Scan-Punkt gehörigen Koordinaten auf dem Bild bezeichnet.
Um die Textur-Koordinaten eines Meßpunktes zu berechnen, soll jeder
Meßpunkt ![]() auf eine virtuelle Ebene
auf eine virtuelle Ebene ![]() projiziert werden (siehe Abbildung 3.12). Dies
geschieht online, also während des Scanvorgangs.
projiziert werden (siehe Abbildung 3.12). Dies
geschieht online, also während des Scanvorgangs.
Um dies zu erreichen, werden zuerst die Winkel ![]() (Winkel
zwischen
(Winkel
zwischen ![]() und der
und der ![]() -Achse) und
-Achse) und ![]() (Winkel zwischen
(Winkel zwischen
![]() und der
und der ![]() -Achse und der
-Achse und der ![]() -Achse, verschoben um die
Kameraposition) berechnet.
-Achse, verschoben um die
Kameraposition) berechnet.
 |
(3.7) | ||
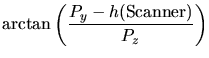 |
(3.8) |
Mit diesen Winkeln wird dann der Punkt auf eine 2 Meter entfernte
Ebene projiziert. Die Projektion
![]() wird in zwei
Projektionen zerlegt, nämlich eine, die in der
wird in zwei
Projektionen zerlegt, nämlich eine, die in der ![]() Ebene abläuft,
und eine, die in der
Ebene abläuft,
und eine, die in der ![]() Ebene abläuft. Das Ergebnis der beiden
Projektionen ergibt sich durch Zusammensetzung der Projektionen.
Ebene abläuft. Das Ergebnis der beiden
Projektionen ergibt sich durch Zusammensetzung der Projektionen.
| (3.9) | |||
| (3.10) |
Anschließend wird das zweidimensionale Abbild des Scans noch so
skaliert, daß Punkte, von denen Texturinformationen vorliegen,
![]() Werte zwischen 0 und 506/1024 und
Werte zwischen 0 und 506/1024 und ![]() Werte zwischen 0 und
997/2048 besitzen. Dabei ist 506
Werte zwischen 0 und
997/2048 besitzen. Dabei ist 506 ![]() 997 die Auflösung des aus
mehereren Fotos bestehenden Bildes und 1024
997 die Auflösung des aus
mehereren Fotos bestehenden Bildes und 1024 ![]() 2048 die Auflösung
der Textur innerhalb des OpenGL Programms (vgl. Abschnitt 6.5.2)
2048 die Auflösung
der Textur innerhalb des OpenGL Programms (vgl. Abschnitt 6.5.2)
Bei dem verwendeten Aufbau exisistiert nicht von allen Punkten eine Texturinformation, da der Öffnungswinkel der Kamera wesentlich kleiner als 180 Grad ist.
Die Flächensegmentierung beruht auf der Annahme, daß eine eingescannte Fläche (z.B. eine Wand) in mehreren -- in etwa aufeinander folgenden -- Scans durch hinreichend nahe übereinander liegende Linien approximiert wird.
Gegeben sei ein Objekt, welches im Sichtbarkeitsbereich des Scanners
liegt. Die erste (unterste) Linie, die zu diesem Objekt gehört, sei
zuerst im ![]() -ten Scan
-ten Scan ![]() sichtbar und werde mit
sichtbar und werde mit ![]() bezeichnet. Wenn in dem darauffolgenden Scan
bezeichnet. Wenn in dem darauffolgenden Scan ![]() die
Prädiktion einer potentiellen Fläche validiert wird, d.h. eine
Linie
die
Prädiktion einer potentiellen Fläche validiert wird, d.h. eine
Linie ![]() existiert, so daß die Endpunkte
beider Linien hinreichend genau übereinstimmen, wird die
Anfangslinie aus Scan
existiert, so daß die Endpunkte
beider Linien hinreichend genau übereinstimmen, wird die
Anfangslinie aus Scan ![]() zu einer Fläche expandiert.
zu einer Fläche expandiert.
Dieser Vergleich der Endpunkt ist in Abbildung 3.14 zu
sehen. Jedoch beschränkt sich der Test nicht nur auf die reine
euklidische Distanz der Endpunkte, sondern schließt auch die Überprüfung des Winkels
![]() zwischen beiden Linien mit ein, der eine Schranke
zwischen beiden Linien mit ein, der eine Schranke
![]() nicht überschreiten darf.
Ansonsten besteht insbesondere bei kürzeren Linien die Möglichkeit, daß sie selbst dann gematcht werden,
wenn ihre Orientierungen stark voneinander differieren.
nicht überschreiten darf.
Ansonsten besteht insbesondere bei kürzeren Linien die Möglichkeit, daß sie selbst dann gematcht werden,
wenn ihre Orientierungen stark voneinander differieren.
Die eigentliche Segmentierung erfolgt in drei Schritten: Gegeben sei ein Scan
![]() , bestimmt durch die darin erkannten Linien. Jede dieser neuen
Linien wird nun wie folgt unterschieden:
, bestimmt durch die darin erkannten Linien. Jede dieser neuen
Linien wird nun wie folgt unterschieden:
Am Ende des Algorithmus sind nun jene Linien, die hinreichend gut eine Fläche in der eingescannten Szene approximieren, nun auch intern zu einer Fläche zusammengefügt. Die in der Szene erkannten Flächen dienen nicht nur der Visualisierung (z.B. durch Einfärbung mittels einer aus dem Kamerabild extrahierten Textur) und der Objektsegmentierung. Sie stellen auch eine ,,Verbindung`` zwischen verschiedenen Scans dar: Marken, die es ermöglichen, mehrere sukzessive aufgenommenen Scans zu einer großen Aufnahme zu vereinen.