3D-Visualisierung

Für die Visualisierung mittels Povray sowie der Mitarbeit an dem OpenGL-Programm danken wir Nicolas Andree.

Im wissenschaftlichen Umfeld bieten sich drei zum Teil grundsätzlich verschiedene Möglichkeiten zur plattformunabhängigen dreidimensionalen Datenvisualisierung an. Diese sind VRML (neu Web3D), OpenGL und Java 3D.

Bei VRML, der Virtual Reality Modelling Language, handelt es sich um ein universelles Dateiformat, welches speziell zum Anzeigen dreidimensionaler Szenen über das Internet entwickelt wurde. Die Anzeige erfolgt durch das Interpretieren von VRML-Dateien durch ein externes Anzeigeprogramm wie z.B. den Cosmo Player. Die Spezifikation von VRML ist auf dessen Homepage einsehbar unter [ URLVrm].

Professionelle Software, bei der eine hohe Performance erreicht werden soll, basiert häufig auf OpenGL, dem eine umfassende API zur schnellen 3D Visualisierung zugrunde liegt. Diese Schnittstelle verfügt über ein Repertoire von über 150 Funktionen mit vielfältigen Möglichkeiten der 2D- und 3D-Visualisierung und wird häufig im Rahmen von CAD Anwendungen oder zur Darstellung dreidimensionaler virtueller Welten eingesetzt. Die Tatsache, daß Grafikkartenhersteller inzwischen Mittelklassekarten mit hardwarebeschleunigten OpenGL-Treibern anbieten, erhöht die Darstellungsgeschwindigkeit nachhaltig und somit die Eignung von OpenGL. Die Programmierung erfolgt in C. Die Homepage von OpenGL findet man unter [ URLOgl]. Unter Linux steht OpenGL als OpenGL-workalike (jedoch ohne Hardwarebeschleunigung) unter dem Namen ,,Mesa`` zur Verfügung. Für weitere Informationen siehe auch [ URLMes].

Java 3D erlaubt es dem Entwickler, seine Applikation im Rahmen der Java Virtual Machine komplett objektorientiert zu entwickeln. Ausgangspunkt der Modellierung von dreidimensionalen Szenen ist hier immer der Szenengraph. Als low-level Schnittstelle zur eigentlichen dreidimensionalen Darstellung wird entweder OpenGL oder aber Direct3D von Microsoft benutzt. Die Programmierung mit Java 3D erfolgt objektorientiert und ist plattformunabhängig. Spezifikationen aller Klassen, weitere Informationen und Tutorien sind auf der Java 3D Homepage unter [ URLJ3D] abrufbar.

Erste Visualisierung der Testdaten

Erste Bilder, die einen Einblick in die Güte der zu erwartenden Ergebnisse liefern sollten, entstanden aufgrund der Vertrautheit mit dem Umgang mit dem Raytracer Povray. Diese Bilder sahen bereits recht vielversprechend aus, vergleiche Abbildung 6.1.

Abbildung 6.1: Erste Darstellung mittels Povray

Die Visualisierung mittels Povray unterliegt jedoch folgenden Nachteilen:

1. Die generierte Beschreibung der Szene muß kompiliert werden. Dieser Vorgang benötigt bei etliche tausend Meßpunkten, die jeweils einzeln durch eine Povray-Primitive repräsentiert werden, mehrere Stunden.
2. Das generierte Sourcefile erreicht leicht eine Größe von mehreren Megabyte.
3. Die gerenderte Szene ist statisch. Um die Szene aus einem geänderten Blickwinkel betrachten zu können, ist es notwendig, die Datei neu zu kompilieren.

Daher haben wir Povray ladiglich als erste, einfache Möglichkeit verwendet, um Scannerdaten zu visualisieren und damit die Machbarkeit des hier vorgestellten 3D-Scanners zu beurteilen.

Für die eigentliche Darstellung der Scannergebnisse benutzen wir OpenGL.

Die Datenstrukturen innerhalb des OpenGL-Programmes

Aus Gründen der Performance sowie aufgrund der einfachen Handhabung in C werden für Datenstrukturen zur Speicherung von Objektdaten wie Koordinaten, Texturdaten, etc. Felder verwendet. Diese werden im Shared Memory abgelegt.

Die Speicherallokation dieser Felder lies sich mit Hilfe der realloc()-Funktion auf eine dynamische Art und Weise realisieren. Dies ist besonders deswegen hervorzuheben, weil bei einer Online-Darstellung des Scannvorganges die Anzahl der eingescannten Meßwerte und damit den benötigten Speicher nicht bekannt ist. Der Speicherbedarf ist enorm, wenn der Scanner in der höchsten Auflösung betrieben wird (113400 Punkte - vgl. Tabelle 3.2). Zu jedem Punkt werden 3 Integer (Koordinaten) und bis zu 4 Floats (Texturkoordinaten, Farbe) abgespeichert.

Benutzerinteraktion

Es wurde eine freie Navigation innerhalb der visualisierten Szene implementiert. Zur Verfügung stehen Bewegungen des Blickpunktes der virtuellen Kamera in alle drei Richtungen des Koordinatensystems, was durch Transformationen realisiert wird. Desweiteren gibt es Rotationen um die $x$-, $y$- und $z$-Achse. Quelltexte findet man in Anhang C.3.1.

Main Eventloop

Wie in fast jedem OpenGL Programm findet man auch hier die beiden Funktionen
glutKeyboardFunc(Key) und glutDisplayFunc(display) in der main()-Funktion. Diese Funktionen befinden sich in einer Eventloop, der glutMainLoop(). Diese ermöglicht es, daß die Änderungen von Statusvariablen unmittelbar in die entsprechende Transformation oder Rotation umgesetzt werden. Mithilfe der Funktion glutReshapeFunc(Reshape), die sich ebenfalls im glutMainLoop() befindet, wird dann die Szene neu gezeichnet.

Übersicht der Funktionalität

In der Scannerapplikation stehen nun die folgenden Visualisierungs-Modi zur Verfügung:

• Anzeigen aller Meßwerte als Punkte,
• Verbinden der Punkte zu einem Drahtgittermodell, sowie die
• Anzeige der Ergebnisse der digitalen Bildverarbeitung. Dazu gehören insbesondere die in der Szene erkannten Linien, Flächen und Objekte.

In jedem dieser Modi kann man sich durch die Szene bewegen, d.h. man kann die Szene aus verschiedenen Perspektiven betrachten.

Das Umschalten zwischen den einzelnen Modi wird durch Betätigen der entsprechenden Tasten realisiert. Hier zunächst eine Übersicht der Darstellungsformen und der zugehörigen Tastaturbelegung:

$$\begin{array}{\vert c\vert c\vert c\vert c\vert} \hline \mb... ...{'p'}&\mbox{'l'} &\mbox{'s'} &\mbox{'o'}\\ \hline \end{array}$$

$$\begin{array}{\vert c\vert c\vert c\vert c\vert} \hline \mb... ...'}&\mbox{'w'}&\mbox{'$\div$', '$\times$'}\\ \hline \end{array}$$

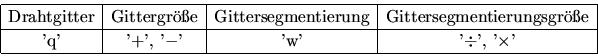
Für die Anzeige stehen grundsätzlich zwei Modi zur Verfügung: Die Objekte können entweder mit Texturen versehen oder gemäß ihres Typs eingefärbt werden. Polygone werden wahlweise offen oder geschlossen dargestellt. Es ist jeweils möglich, zwischen diesen hin- und herzuschalten.

$$\begin{array}{\vert c\vert c\vert c\vert c\vert c\vert c\ver... ...{'b'}&\mbox{'r'} &\mbox{'n'} &\mbox{'h'}\\ \hline \end{array}$$

Folgende Funktionen sind zur Navigation in der Szene gedacht. Mit Benutzung des numerischen Tastenblocks ist eine recht intuitive Bewegung möglich. Die Rotationen beziehen sich immer auf den Koordinatenursprung.

$$\begin{array}{\vert c\vert c\vert c\vert} \hline \mbox{Rota... ...ownarrow &\leftarrow, \rightarrow & 7, 1 \\ \hline \end{array}$$

$$\begin{array}{\vert c\vert c\vert c\vert} \hline \mbox{Tran... ...z$-Richtung}\\ \hline 4, 6& 8, 2 & 9, 3 \\ \hline \end{array}$$

Punktedarstellung

Es gibt zwei alternative Arten von Punktvisualisierungen.

• Zum Anzeigen aller Meßpunkte wird die OpenGL-Primitive GLPoints benutzt. Um dies zu ermöglichen, werden die Punkte aus der Pipeline oder aus der Datei Points.ogl importiert. Intern sorgt der Aufruf der Funktion DrawPoints() für das Ausführen der Darstellung.

• Zur Visualisierung der reduzierten Datenmenge wie in Kapitel 3.2.1 beschrieben wird auf die OpenGL-Primitive GLQuads zurückgegriffen, Punkte werden somit als kleine Flächen dargestellt. Dies geschieht mit Hilfe der Funktion DrawQuads() (vgl. Anhang C.3.2 für den Quelltext).

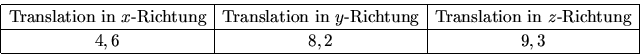
  Die Funktion DrawQuads() ist allgemein gehalten, kann daher bei anderer Parametrisierung auch für die Darstellung von Polygonen wie Flächen, Objekten und Linien (auch dargestellt als Polygone) verwendet werden. Es stehen zwei Polygondarstellungsmodi ,, Polygone offen`` und ,, Polygone gefüllt`` zur Auswahl. Die Darstellung durch offene Polygone ist sinnvoll, um ansonsten verborgene Punkte visualisieren zu lassen.

Linien-, Flächen- und Objektdarstellung

Zum Anzeigen von Linien und Flächen gibt es wieder je zwei Modi, die die Abhängigkeit zeigen, wie weit beispielsweise Linien in der nächsten Stufe der Bildverarbeitung durch Flächen oder Objekte gematcht werden. Insgesamt kommen die in der Tabelle verzeichneten Fälle vor:

$$\begin{array}{\vert c\vert c\vert c\vert} \hline \mbox{Lini... ...nicht zu Objekten gematchte} &\mbox{\%} \\ \hline \end{array}$$

Die Idee dabei ist, daß die in der nächsten Stufe der Bildverarbeitung nicht gematchten Linien beispielsweise als Information beim Aktivieren des Anzeigens der nächsten Stufe (z.B. die Flächen) zusätzlich sichtbar gemacht werden können. Diese Information steht dem Betrachter also auch weiterhin zur Verfügung. Die einzelnen Linien, Flächen und Objekte werden nun wieder von der Funktion DrawQuads() gezeichnet.

Drahtgittermodell

Die Wahl des Modes der Polygondarstellung spielt auch bei der Drahtgitterdarstellung eine Rolle, da sie mit Hilfe der OpenGL-Primitive GLQuadStrip realisiert wurde.

Abbildung 6.2: Funktionsweise der OpenGL-Primitive GLQuadStrip.

Primär ist die Funktion DrawQuadStrip() für die Drahtgitterdarstellung verantwortlich. Mittels den Tasten '+', '-' knan die Grösse des Drahtgitters angepasst werden.

Im Modus ,, Polygone geschlossen`` entsteht eine homogene Fläche. Aus diesem Grunde wird das Textur-Mapping von dem Mode ,, Polygone geschlossen`` natürlich begünstigt, da keine Lücken mehr auftreten können, wie dies z.B. bei einer reinen Punktedarstellung noch möglich ist.

Segmentierung im Drahtgittermodell

Man kann sich überlegen, daß Objekte im Drahtgittermodell durch einen langgestrekten QuadStrip verbunden sind. Dies liegt daran, daß die Tiefeninformation stark schwankt.

Die Idee ist nun, diese Eigenschaft auszunutzen, um einen einfachen Segementierer zu programmieren. Dabei werden einfach entartete Quadstrips, also Quadstrips, mit zu langen Diagonalen, nicht gezeichnet. Mit 'w' läßt sich ein solcher einfacher Segmentierer ein/ausschalten, mit '$\div$' und '$\times$' kann man den Schwellenwert für die Länge der Diagonalen variieren. Abbildung 6.3 zeigt einen Ausschnitt eines Scans mit und ohne Segmentierung (der Blickpunkt wurde etwas zur Seite verschoben, damit man die Tiefeninformation besser sieht). Man erkennt, daß die Umrisse der gescannten Person klar zu sehen sind. Weitere Bilder befinden sich in Abschnitt 6.6.

Mit diesem Ansatz alleine lassen sich jedoch naturgemäß nicht alle Objekte korrekt segmentieren. So sind zum Beispiel lange Kanten eines Objektes, die parallel zur Laserrichtung verlaufen, problematisch. Weiterhin ist bisher nicht berücksichtigt, daß weit entfernte Scanpunkte einen größeren Abstand zu den Nachbarpunkten aufweisen. Diese werden demzufolge auch segmentiert.

Abbildung 6.3: Die Drahtgittersegmentierung

Datenimport

Es gibt die Möglichkeit, die Daten bereits während des Scanvorgangs im Online-Anzeigemodus aus der Pipeline einzulesen und anzuzeigen. Der Import der eingescannten Daten erfolgt dann entweder direkt aus einer Pipeline oder aus den beiden Dateien Data.ogl und Points.ogl.

Online-Anzeige

Um die Online Anzeige zu ermöglichen, ist es notwendig, die Einlesefunktion als einen weiteren Prozeß innerhalb des Anzeigeprogramms zu deklarieren. Aus der Scanner-Pipeline werden die Daten in die entsprechenden Felder kopiert und parallel durch die Display Funktionen angezeigt. Die Felder befinden sich im Shared Memory. Während dieses Einlesens wachsen die Felder inkrementell. Bei der Online-Ausgabe wird, um bessere Performance zu erhalten, die OpenGL Darstellung nur aller 2 Sekunden aktualisiert.

Falls die Daten bereits vorliegen und kein Online-Betrieb durchgeführt wird, können die Daten aus den Dateien Data.ogl und Points.ogl eingelesen werden. Für die Daten aus Points.ogl ist es ebenfalls möglich, den schrittweisen, dynamischen Aufbau der Szene Scan für Scan wie im Online-Modus mitzuverfolgen.

Gleichzeitig erfolgt der Import der Daten, die in vorigen Programmteilen bearbeitet wurden, aus der Datei Data.ogl. Diese Aufgabe erfüllt die Funktion read_file(). Dieser Import umfaßt alle Linienkoordinaten, Punkte, die nicht auf erkannten Linien liegen, erkannte zusammenhängende Flächen sowie die Ergebnisse der Objekterkennung.

Texturen in OpenGL

Das OpenGL Anzeigeprogramm liest die jpeg-Bilder der Größe 506 $\times$ 997 in ein RGBA-Array der Größe 1024 $\times$ 2048. Dabei werden mehrere Fotos zu einem Bild zusammengefügt. Das etwas größere Array wurde zuvor mit einem einheitlichen Farbwert (Hellgrau) gefüllt. Das Einlesen geschieht derart, daß die linke untere Ecke des Bildes den Arrayindex (1,1) bekommt. Dadurch entsteht ein 1 Pixel breiter Rand an der linken und unteren Bildkante.

Abbildung 6.4: Die Texture in OpenGL

OpenGL stellt einfach zu handhabende Routinen zur Textur-Verarbeitung zur Verfügung. Jedem Punkt ( glVertex3f) kann eine Textur-Koordinate mit dem Befehl glTexCoord2f zugeordnet werden. Das Mapping der Texturen geschieht dann automatisch. Die Argumente der Funktion glTexCoord2f sind zwei Floatingpoint-Zahlen zwischen 0 und 1, die die Position in dem Textur-Array spezifizieren. Falls bei dem Initialisierungsbefehl glTexParameteri die Einstellung GL_CLAMP angegeben wurde, wird bei Textur-Koordinaten außerhalb des Bereiches (0,1) das jeweils letzte Pixel innerhalb der Textur kopiert. Dies erklärt den ein-Pixel breiten Rand um die eigentliche Textur. Dadurch wird sichergestellt, daß alle Bereiche, von denen keine Textur-Informationen vorliegen, einheitlich eingefärbt werden.

Aufbau der Datenaustausch-Dateien

Zunächst die BNF für grundlegende Daten und Objekte:

   <Int>          ::= <IntDigit> | +<IntDigits> | -<IntDigit>.
   <IntDigits>    ::= `1' | `2' | ... | `0' | <IntDigits>
                      <IntDigits>.
   <Double>       ::= <DoubleDigits> | +<DoubleDigits> | 
                      -<DoubleDigits>.
   <DoubleDigits> ::= <IntDigits> | <IntDigits>.<IntDigits>. | 
                      .<IntDigits>.

   <Objekt>       ::= <Fläche> <NL> <Fläche>.
   <Fläche>       ::= <Linie> <NL> <Linie>.
   <Linie>        ::= <Punkt> <NL> <Punkt>.

   <Punkt>        ::= <Int> <K> <Int> <K> <Int> <K> <Double> 
                      <K> <Double>.

   <K>            ::= `,'.
   <NL>           ::= `\n'.

Syntax von Points.ogl

Die Datei Points.ogl beinhaltet alle eingescannten Meßpunkte. Der Aufbau der Datei ist sehr einfach. Jede Zeile enthält genau einen Meßpunkt. Die Speicherung folgt der Reihenfolge, in der die Daten eigescannt wurden, so daß die vorgegeben Ordnung erhalten bleibt.

Der Integerwert in der ersten Zeile gibt an, wieviele Punkte sich jeweils in einem Scan befinden. Die Datei hat somit folgende Struktur:

   <File>         ::= `0' | <Int> <NL> <Points>.
   <Points>       ::= <Punkt> | <Punkt> <NL> <Points>.

Syntax von Data.ogl

Zu Beginn steht die Anzahl der jeweils von diesem Typ anzuzeigenden Werte sowie ein String, um welchen Typ es sich handelt. Als Typ stehen ,,Points``, ,,Lines``, ,,Surfaces`` und ,,Objects`` zur Auswahl. Das bedeutet, wenn beispielsweise der String ,,Surfaces``$\,$ gelesen wird, alle nachfolgenden Daten (bis zu dem nächsten typisierenden String) als Flächen nach der angegebenen Syntax zu interpretieren sind.

   <File>         ::= <Points> <NL> <Lines> <NL> <Surfaces> 
                      <NL> <Objects>.
   <Points>       ::= `0 Points' | <Int> `Points' <NL> <P>.
   <P>            ::= <Punkt> <NL> <P> | <Punkt>.
   <Lines>        ::= `0 Lines' | <Int> `Lines' <NL> <L>.
   <L>            ::= <Linie> <NL> <L> | <Linie>.
   <Surfaces>     ::= `0 Surfaces' | <Int> `Surfaces' <NL> <S>.
   <S>            ::= <Fläche> <NL> <S> | <Fläche>.
   <Objects>      ::= `0 Objects' | <Int> `Objects' <NL> <O>.
   <O>            ::= <Objekt <NL> <O> | <Objekt>.

Die vollständige Beschreibung eines Punktes besteht hier also aus drei Integern für die Raumkoordinaten im $\mathbbm{R}^3$, zwei Floats für die Textur-Koordinaten und drei weiteren Floats für eine alternative Farbgebung. Zur Beschreibung einer Linie werden zwei Punkte, zur Beschreibung von Flächen vier Punkte und zur Darstellung von Objekten acht Punkte benötigt. Für einen beispielhaften Aufbau der Dateiformate siehe auch Anhang C.4.

Screenshots des 3D-Outputs

Auf den nachfolgenden Seiten sind nun einige Screenshots von Beispiel-Scans zu sehen: die Bilder sind bei einem Gang durch ein Gebäude aufgenommen worden und zeigen anschaulich die aktuellen Möglichkeiten des vorgestellten 3D-Laserscanners.

Anhand dieser ersten Szene werden im folgenden die verschiedenen Visualisierungsmöglichkeiten dargestellt. Zunächst sind die reinen Scanpunkte zu sehen, die von der 3D-Scannerhardware geliefert werden. Bemerkenswert ist die optisch schon recht gute Qualität, die sich schon nach einer simplen Koordinatentransformation (siehe Abschnitt 3.2.2) ergibt.

Die - gerade an den Seiten - sichtbare Krümmung stammt von der Drehbewegung des Scanners um seine $X$-Achse. Offentsichtlich beschreibt der Auftreffpunkt des Lasersstrahls eine halbkreisförmige Bahn auf einer in Blickrichtung des Scanners verlaufenden Ebene.

Auf der rechten Seite des Bildes sind zwei horizontale Störungen zu sehen, d.h. die Wand erscheint an diesen Stellen unterbrochen und die zugehörigen Scanpunkte sind nach vorne versetzt. Dies entstand durch zwei Personen, die während des Scannens duch den Flur gelaufen sind. Die dabei auftretenden Veränderungen sind in Abbildung 6.5 verdeutlicht.

Abbildung 6.5: Vorbeilaufen eines Menschens auf der rechten Seite (von hinten kommend)

Im Gegensatz zur reinen Punktedarstellung des letzten Bildes erlaubt die in Abschnitt 3.2.1 geschilderte Reduktion der Daten, diese als kleine Vierecke mit konfigurierbarer Größe darzustellen, ohne auf akzeptable Performance verzichten zu müssen.

Die folgenden Bilder visualisieren die Ergebnisse des Linienerkennungs-Algorithmus. Dabei mußten empirische Schwellwerte so eingestellt werden, daß auch recht kurze Linien als solche erkannte werden (vergleiche nächste Bilder).

Die erkannten Linien werden zu Flächen zusammengefaßt. Schön zu sehen ist die große Fläche auf der linken Seite. Die Person in der Mitte ist nun als ein lose zusammemnhängender Haufen unterschiedlich orientierter, kleinerer Flächen sichtbar.

Legt man die erkannten Flächen über die Scandaten, läßt sich anschaulich die Korrektheit des Flächenerkennungs-Algorithmus plausibel machen. Die Reihe unzusammenhängender Flächen auf der rechten Seite haben Ihren Ursprung in den bereits erklärten Störungen durch Personen, die durch die Szene gelaufen sind. Dies soll als Beispiel dafür dienen, daß die hier vorgestellten Algorithmen sehr robust gegen diese Art von Umgebungsveränderungen ist.

Die aus diesen Flächen entstehenden Objektbegrenzungen reichen trotz der Bilstörungen zur sicheren Hindernis-Vermeidung aus.

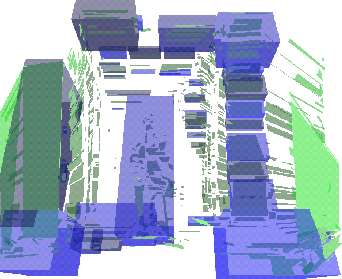
Größere Flächen wie die linke Wand werden als eigenständige Objekte betrachtet, kleinere Flächen werden zu größeren Objekten zusammengefügt, sofern sie hinreichend eng beieinander liegen. Die Objekte werden durch die sie begrenzenden Boundingboxes dargestellt.

In dieser Ansicht sieht man sehr gut, wie die Person in der Mitte vollständig von einer Box umschlossen wird.

In dieser etwas geänderten Ansicht ist die dreidimensionale Struktur der Szene sichtbar. Man erkennt, daß die Elemente (und insbesondere die Person) wirklich durch dreidimensionale, abgeschlossene Objekte repräsentiert werden.

Solch eine reine Objektdarstellung eignet sich als eine dreidimensionale Belegtheitskarte des gescannten Raumes, beispielsweise zur Roboternavigation.

Darstellung der gescannten Szene von oben. Im Gegensatz zu einfachen 2D-Laserscannern - mit denen eine ähnliche Darstellung auch zu erreichen gewesen wäre - ist es hier möglich, Objekte wie Boxen, Eimer, Stühle etc. aufgrund ihrer geringen Höhe und Ausmaße als Einrichtungsgegenstände des Raumes zu identifizieren. Zweidimensionalen Scannern fällt es schwer, zwischen dem Raum selber und solchen Gegenständen zu unterscheiden, so daß selbst in solch einfachen Kartographie-Einsätze der 3D-Laserscanner eindeutig von Vorteil ist.

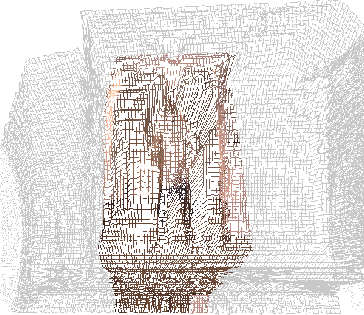
Eine weitere Möglichkeit der Darstellung ist das Drahtgitter: Dazu werden Scandaten (mit veränderbarer Auflösung quantifiziert) als Punkte genommen, die untereinander verbunden werden (vergleiche auch Seite ).

Ferner kann das Drahtgitter mit einer Textur belegt werden, die aus den während des Scans aufgenommenen Fotos berechnet wird. Gescante (Rand-)Gebiete, die nicht von den Fotos abgedeckt werden, sind grau dargestellt.

Mithilfe des Drahtgitters bietet sich ebenfalls eine einfache Möglichkeit der Segementierung: Hierzu werden die Facetten des Drahtgitters nur dann gezeichnet, wenn ihre Diagonalen einen Schwellwert nicht überschreiten.

Dieser Schwellwert läßt sich interaktiv anpassen, das Resultat ist eine Segmentierung der Person in der Mitte des Ganges.

Werden nun die Facetten des Gitters ausgefüllt gezeichnet, lassen sich die segmentierten Objekte komplett mit ihren Texturen überziehen.

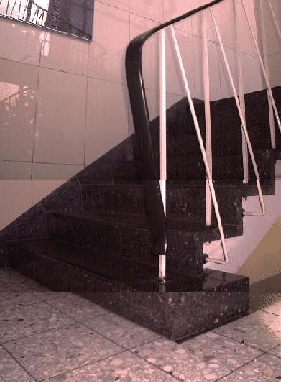
Ein neues Szenario: Aufnahmen einer Treppe. Rechts ein Foto der Szene, zusammengesetzt aus drei Kamera-Aufnahmen. Links das Ergebnis eines 3D-Scans.

Anhand dieser frontalen Ansicht der Treppe läßt sich gut die Fähigkeit des Drahtgitter-Segmentierers aufzeigen.

Es ist möglich, selbst die einzelnen Treppenstufen als voneinander getrennte Bereiche zu erkennen.