Rotation und Euler Winkel

Eine $3 \times 3$ Rotationsmatrix $\MR$ kann durch drei Euler Winkel $\theta_x, \theta_y, \theta_z$, die einer Drehung um die $x, y$ und $z$-Achse entsprechen, ausgedrückt werden [20]. Die orthonormale Matrix $\MR$ wird durch

$$\MR= \MR_x \MR_y \MR_z$$ (3.1)

berechnet, wobei

$$\MR_x = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \theta_x & -\sin \theta_x \\ 0 & \sin \theta_x & \cos \theta_x \\ \end{array}\right)$$

ist und $\theta_x$ den Winkel der Drehung um die $x$-Achse bezeichnet. Die Matrizen $\MR_y, \MR_z$ sind analog definiert:

$$\MR_y = \left( \begin{array}{ccc} \cos \theta_y & 0 & -\sin \thet... ...& 0 \\ \sin \theta_z & \cos \theta_z & 0 \\ 0 & 0 & 1 \\ \end{array}\right).$$

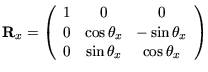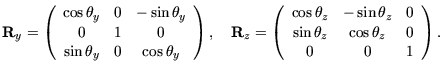Damit ergibt sich die Rotationsmatrix als

$$\MR= \left( \begin{array}{ccc} \cos \theta_y \cos \theta_z & ... ... \theta_z & \cos \theta_x \cos \theta_y \\ \end{array}\right).$$

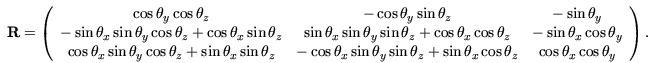Bei der Darstellung einer Rotationsmatrix mittels Euler-Winkel ist zu beachten, dass die Reihenfolge der Multiplikationen in (3.1) eine entscheidende Rolle spielt: Das Ergebnis einer Drehung hängt im Allgemeinen davon ab, um welchen Euler Winkel zuerst rotiert wird.