


Next: Matching als Optimierungsproblem
Up: Darstellung von Rotationen und
Previous: Rotation und Euler Winkel
Neben der Repräsentation einer Rotation mit Hilfe der Euler Winkel
wird das so genannte Einheitsquaternion (engl.: unit
quaternion) eingesetzt [20]. Das Quaternion beschreibt
eine Rotation um einen Vektor, der durch den Ursprung des Koordinatensystems
geht. In Abbildung 3.1 sind ein Einheitsvektor
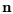 und
ein Winkel
und
ein Winkel 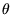 dargestellt, die die Rotation der beiden
Koordinatensysteme beschreiben. Das blaue Koordinatensystem ist das
Ergebnis der Drehung des schwarzen Systems um einen Winkel
dargestellt, die die Rotation der beiden
Koordinatensysteme beschreiben. Das blaue Koordinatensystem ist das
Ergebnis der Drehung des schwarzen Systems um einen Winkel 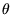 .
.
Abbildung 3.1:
Quaternion zur Beschreibung einer Rotation
|
|
Das Quaternion geht auf Hamilton zurück und kann mathematisch als eine
komplexe Zahl mit drei verschiedenen imaginären Anteilen behandelt
werden (siehe Anhang A.1) [1,34]:
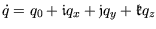 mit mit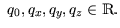 |
|
|
|
Bei gegebenem Einheitsvektor
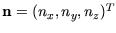 und Rotationswinkel
und Rotationswinkel 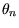 lässt sich das Einheitsquaternion
berechnen durch [10,20]:
lässt sich das Einheitsquaternion
berechnen durch [10,20]:
Die Rotationsmatrix berechnet sich aus einem Einheitsquaternion 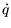 wie folgt:
wie folgt:
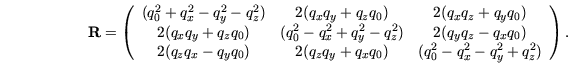 |
|
|
(3.6) |
Dass eine Rotation in dieser Form dargestellt werden kann, geht aus
den Beweisen in Anhang A.1.1 und A.1.2 hervor. Die
Verwendung des Einheitsquaternions zur Darstellung von Rotationen
garantiert, dass die entsprechende Rotationsmatrix orthonormal ist.



Next: Matching als Optimierungsproblem
Up: Darstellung von Rotationen und
Previous: Rotation und Euler Winkel
Andreas Nüchter
2002-07-10
![]() und
ein Winkel
und
ein Winkel ![]() dargestellt, die die Rotation der beiden
Koordinatensysteme beschreiben. Das blaue Koordinatensystem ist das
Ergebnis der Drehung des schwarzen Systems um einen Winkel
dargestellt, die die Rotation der beiden
Koordinatensysteme beschreiben. Das blaue Koordinatensystem ist das
Ergebnis der Drehung des schwarzen Systems um einen Winkel ![]() .
.