Berechnung des Einheitsquaternion

Ein Vektor $\mathbf{v}= (v_x,v_y,v_z)^T \in \mathbbm{R}^3$ soll um einen Vektor $\mathbf{n}$ um den Winkel $\theta$ gedreht werden. Diese Drehung wird durch das Einheitsquaternion $\dot q = q_{0} + \mathbf{q} \cdot \boldsymbol{\mathfrak{i}}$ mit $q_0 = \cos \frac{\theta}{2}$ und $\mathbf{q}= \mathbf{n}\sin \frac{\theta}{2}$ beschrieben. Eine Möglichkeit, den gesuchten Punkt $\mathbf{v}_{rot}$ zu errechnen, ist die im vorigen Abschnitt vorgestellte Methode, das Quaternion $\dot v$ des Vektors $\mathbf{v}$ mit $\dot q$ und $\dot q^*$ zu multiplizieren (vgl. (A.11)):

$$\mathbf{v}_{rot} = \dot q \dot v \dot q^*$$

$$= \left(\cos\frac{\theta}{2}, \mathbf{n}\sin\frac{\theta}{2}\right)... ...bf{v}\right) \left(\cos\frac{\theta}{2}, -\mathbf{n}\sin\frac{\theta}{2}\right)$$

$$= \left(\left(\cos\frac{\theta}{2}, \mathbf{n}\sin\frac{\theta}{2}\... ...ght)\right) \left(\cos\frac{\theta}{2}, -\mathbf{n}\sin\frac{\theta}{2}\right).$$

Daraufhin wird die Quaternionmultiplikation (vgl. (A.4)) angewendet und es ergibt sich:

$$\mathbf{v}_{rot} = \left(-\sin\frac{\theta}{2}(\mathbf{n}\cdot \mathbf{v}), \cos\fra... ...f{n})\right) \left(\cos\frac{\theta}{2}, -\mathbf{n}\sin\frac{\theta}{2}\right)$$

$$= \left( -\sin\frac{\theta}{2}\cos\frac{\theta}{2}(\mathbf{n}\cdot ... ... -\sin^2\frac{\theta}{2}(\mathbf{n}\times \mathbf{v}) \cdot \mathbf{n}, \right.$$

$$\sin^2\frac{\theta}{2}(\mathbf{n}\cdot \mathbf{v}) \mathbf{n} +\c... ...hbf{v}) - \sin\frac{\theta}{2}\cos\frac{\theta}{2}(\mathbf{v}\times \mathbf{n})$$

$$\left. - \sin^2\frac{\theta}{2}(\mathbf{n}\times \mathbf{v}) \times \mathbf{n} \right).$$ (7.12)

Benutzt man nun einige Fakten über Vektoren (dass $\mathbf{n}\cdot \mathbf{v}= \mathbf{v}\cdot \mathbf{n}$, $\mathbf{n}\times \mathbf{v}= - \mathbf{v}\times \mathbf{n}$ und $(\mathbf{n}\times \mathbf{v}) \cdot \mathbf{n}= 0$ ist) und bezieht die folgenden trigonometrischen Identitäten mit ein:

$$\cos \theta = \cos^2 \frac{\theta}{2} - \sin^2\frac{\theta}{2}$$

$$\sin \theta = 2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}$$

$$\cos \theta = 1 - 2 \sin^2\frac{\theta}{2},$$

so ergibt sich für (A.12):

$$\mathbf{v}_{rot} = \left( 0, \sin^2\frac{\theta}{2}(\mathbf{n}\cdot \mathbf{v}) \mat... ...n^2\frac{\theta}{2}(\mathbf{v}- (\mathbf{n}\cdot \mathbf{v}) \mathbf{n} \right)$$

$$= \left( 0, 2 \sin^2\frac{\theta}{2}(\mathbf{n}\cdot \mathbf{v}) \m... ... \sin\frac{\theta}{2}\cos\frac{\theta}{2}( \mathbf{n}\times \mathbf{v}) \right)$$

$$= \left( 0, (1 - \cos\theta)(\mathbf{n}\cdot \mathbf{v})\mathbf{n} + \cos \theta \mathbf{v}+ \sin \theta (\mathbf{n}\times \mathbf{v}) \right)$$

$$= \left( 0, (\mathbf{n}\cdot \mathbf{v})\mathbf{n} + \cos \theta (\... ...ot \mathbf{v}) \mathbf{n}) + \sin \theta (\mathbf{n}\times \mathbf{v}) \right).$$ (7.13)

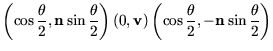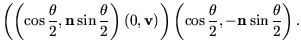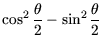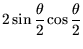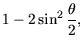Die Formel (A.13) wird nun durch eine grafische Herleitung bewiesen. Die linke Seite der Abbildung A.1 zeigt einen Vektor $\mathbf{v}$, der um den Winkel $\theta$ rotiert wird. Es sei $\mathbf{n}$ ein Einheitsvektor. Die Vektoren $\mathbf{n}$ und $\mathbf{v}$ spannen eine Ebene auf. Auf dieser Ebene liegen die Vektoren $\mathbf{v}_1 = (\mathbf{n}\cdot \mathbf{v}) \mathbf{n}$ und $\mathbf{v}_2 = \mathbf{v}- (\mathbf{n}\cdot \mathbf{v}) \mathbf{n}$. Der Vektor $\mathbf{v}_3$ steht senkrecht zu dieser Ebene und hat die gleiche Länge wie Vektor $\mathbf{v}_2$. Der Vektor lässt sich berechnen durch $\mathbf{v}_3 = \mathbf{n}\times \mathbf{v}_2 = \mathbf{n}\times \mathbf{v}$, da $\mathbf{n}$ ein Einheitsvektor ist und $\mathbf{v}_2 \bot \mathbf{n}$ ist.

Abbildung: Grafische Herleitung des rotierten Vektors $\mathbf{v}_{rot}$

Damit lässt sich der Vektor $\mathbf{v}_{rot}$ schreiben als

$$\mathbf{v}_{rot} = \mathbf{v}_1 + \cos \theta \mathbf{v}_2 + \sin \theta \mathbf{v}_3$$

$$= (\mathbf{n}\cdot \mathbf{v}) \mathbf{n}+ \cos \theta (\mathbf{v}-... ...bf{n}\cdot \mathbf{v}) \mathbf{n}) + \sin \theta (\mathbf{n}\times \mathbf{v}).$$ (7.14)

Wie man nun sieht entspricht die Formel (A.14) genau dem Quaternion $\dot v$ (A.13). Dies zeigt, dass die angegebene Beschreibung der Rotation mittels des Einheitsquaternions (3.2),(3.3),(3.4),(3.5) tatsächlich eine Rotation um einen gegeben Vektor darstellt.