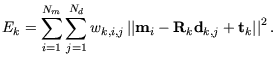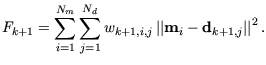


Next: Performanz des iterativen Algorithmus
Up: Matching als Optimierungsproblem
Previous: Matching als Optimierungsproblem
Gegeben sei eine Menge von 3D-Punkten
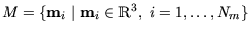 . Für einen 3D-Scan mit der Datenmenge
. Für einen 3D-Scan mit der Datenmenge
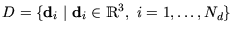 sind eine
Rotation
sind eine
Rotation 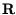 sowie eine Translation
sowie eine Translation
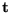 gesucht, die beide Mengen
korrekt ineinander abbilden. Dabei muss die Fehlerfunktion
gesucht, die beide Mengen
korrekt ineinander abbilden. Dabei muss die Fehlerfunktion
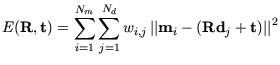 |
|
|
(3.7) |
minimiert werden. 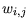 nimmt hierbei den Wert 1 an, falls die
Messpunkte
nimmt hierbei den Wert 1 an, falls die
Messpunkte
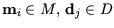 den gleichen Punkt darstellen.
Die Minimierung von (3.7) muss mit der Maximierung von
den gleichen Punkt darstellen.
Die Minimierung von (3.7) muss mit der Maximierung von
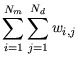 |
|
|
(3.8) |
einhergehen. Trifft dies nicht zu, ist die triviale Lösung
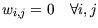 zulässig, was der Idee des Scanmatchings
widerspricht.
zulässig, was der Idee des Scanmatchings
widerspricht.
Der iterative Algorithmus der nächsten Punkte (engl.: iterative
closest points (ICP)) wurde etwa zeitgleich von
Besl/McKay [10], Zhang [85] und
Cheng/Medioni [13] 1991 entwickelt. Der Algorithmus - im
Folgenden mit ICP bezeichnet - stellt einen allgemeinen Rahmen für die
Registrierung von 3D-Tiefenbildern dar. Die fundamentalen Schritte
des Algorithmus sind:
Es kann nachgewiesen werden, dass der obige Algorithmus konvergiert
und ein lokales Minimum findet [10].
Satz 1 (Konvergenz-Theorem)
Der iterative Algorithmus der nächsten Punkte konvergiert monoton zu
einem lokalen Minimum, wenn die Fehlerfunktion
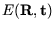
(
3.7) gegeben ist [
10].
Beweis:Der Beweis wird mit vollständiger Induktion geführt. Für alle Iterationen
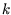 des Algorithmus, insbesondere für den Induktionsanfang
des Algorithmus, insbesondere für den Induktionsanfang 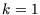 ,
gelten folgende Aussagen: Gegeben seien zwei Mengen
,
gelten folgende Aussagen: Gegeben seien zwei Mengen 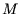 und
und 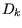 . Der
erste Schritt des obigen Algorithmus liefert die Paare
. Der
erste Schritt des obigen Algorithmus liefert die Paare 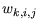 ,
die den Fehler
,
die den Fehler 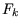 aufweisen:
aufweisen:
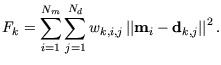 |
|
|
(3.9) |
Schritt 2 des Algorithmus sucht die Transformation (
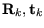 ),
die, angewendet auf die Datenpunkte
),
die, angewendet auf die Datenpunkte
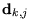 ,
, 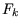 minimiert.
Dadurch wird (3.9) zu
minimiert.
Dadurch wird (3.9) zu
Offensichtlich gilt immer
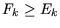 . Angenommen dies wäre nicht der
Fall und es gälte
. Angenommen dies wäre nicht der
Fall und es gälte 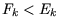 , dann würde die Identitätstransformation
(
, dann würde die Identitätstransformation
(
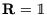 und
und
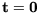 ) in einem kleineren Fehler
) in einem kleineren Fehler 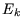 resultieren. Als nächstes wendet man die gefundene Transformation auf
resultieren. Als nächstes wendet man die gefundene Transformation auf
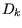 an, wodurch die Menge
an, wodurch die Menge 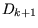 entsteht. Nun werden die Paare
entsteht. Nun werden die Paare
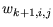 berechnet und es ergibt sich folgender neuer Fehler:
berechnet und es ergibt sich folgender neuer Fehler:
Es gilt
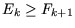 , weil entweder neue Paare mit kleineren
Abständen
, weil entweder neue Paare mit kleineren
Abständen
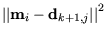 entstehen oder die vorige
Paarung wiederholt wird.
entstehen oder die vorige
Paarung wiederholt wird.
Also ist:
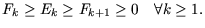 |
|
|
(3.10) |
Aus dem Satz der Konvergenz einer beschränkten monotonen Folge ergibt
sich die Konvergenz zu einem Minimum [23].
Unterabschnitte



Next: Performanz des iterativen Algorithmus
Up: Matching als Optimierungsproblem
Previous: Matching als Optimierungsproblem
Andreas Nüchter
2002-07-10
![]() . Für einen 3D-Scan mit der Datenmenge
. Für einen 3D-Scan mit der Datenmenge
![]() sind eine
Rotation
sind eine
Rotation ![]() sowie eine Translation
sowie eine Translation
![]() gesucht, die beide Mengen
korrekt ineinander abbilden. Dabei muss die Fehlerfunktion
gesucht, die beide Mengen
korrekt ineinander abbilden. Dabei muss die Fehlerfunktion