Ergebnisse des Scanmatchings als Optimierungsproblem

Die vorgestellten Verfahren zur Bildung von Punktpaaren werden in zahlreichen Experimenten untersucht, wobei dazu auch Verfahren kombiniert werden. Die Experimente finden im GMD-Robobench, einem erweiterten Bürotrakt statt (FhG-AIS Gebäude C2 Erdgeschoss). Über einen langen Flur sind dort Büros miteinander verbunden. Der Roboter steht im Flur und nimmt einen 3D-Scan von 180 $\times$ 256 Punkten auf. Anschließend fährt er 2 Meter den Flur entlang und nimmt einen weiteren 3D-Scan auf. Das Scanmatching wird mit dem ICP-Algorithmus solange durchgeführt, bis die Änderung des mittleren Fehlers, also des Fehlers je Punktpaar, kleiner als 0.0001 Zentimeter ist. Eine so kleine Veränderung der Fehlerfunktion deutet auf ein lokales Minimum oder Plateau hin. Der Roboter bestimmt zunächst seine Position mittels der Odometrie. Diese Schätzung ergibt nach der 2-Meter-Fahrt die Werte $(x,y,\theta) = (27.10,\ 233.20,\ 6.64)$, die als Startwert für den ICP dienen. Der ICP-Algorithmus bildet nur Punktpaare, falls der Abstand zwischen den nächsten Punkten kleiner als 25cm ist, d.h.

$$w_{i,j} = \left\{ \begin{array}{lll} &1 \qquad &\mbox{wenn d... ...als 25cm beträgt,} \\ & 0 & \mbox{sonst}. \end{array}\right.$$

Mit einem solchen harten Schwellenwert kann es sein, dass sich die Anzahl der gebildeten Punktpaare ( $\sum_{i=1}^{N_m}\sum_{j=1}^{N_d}w_{i,j}$ (3.8)) verringert. Versuche bestätigen aber, dass durch diese Einschränkung das gesuchte Minimum schneller gefunden wird und man bessere Ergebnisse erhält. (Die Ungleichungskette (3.10) im Konvergenzbeweis ist in diesem Fall nicht erfüllt; Experimente zeigen aber, dass der Algorithmus trotzdem konvergiert.)

Abbildung 3.4 zeigt exemplarisch, wie mit dem ICP Algorithmus zwei 3D-Scans ineinander geschoben, also registriert werden. Weitere Abbildungen und Animationen befinden sich auf der CD.

Abbildung 3.4: Visualisierung der Ergebnisse des ICP-Algorithmus. Die anfängliche Lage zweier 3D-Scans und die nach der ersten, dritten und 10. Iteration sind dargestellt. In jedem Iterationsschritt wird eine Rotation $\MR$ und Translation $\mathbf{t}$ errechnet und auf den zweiten 3D-Scan angewendet.

Tabelle 3.1 stellt die Ergebnisse der Verfahren zur Punktpaarbildung gegenüber. Es wird die zur Bildung der Punktpaare benutzte Methode mit der dafür benötigten Zeit angegeben. Die Zeiten wurden auf einem Pentium III mit 600MHz gemessen. Zusätzlich sind die Anzahl der Iterationen, die nötig waren um das Konvergenzkriterium zu erfüllen, der mittlere Fehler $E(\MR,\mathbf{t})$ (3.7) sowie die Endposition des Roboters angegeben.

Tabelle 3.1: Vergleich der Methoden zur Bildung von Punktpaaren; Ausgangsposition des ICP-Algorithmus ist die auf Odometrie-Daten beruhende Roboterposition $(x,y,\theta) = (27.10,\ 233.20,\ 6.64)$.

Methode	Zeit	Iterationen	Fehler	Endkoordinaten
I - alle Punkte & brute force Suche	3h 47m	27	8.24	(4.53, 221.00, -0.06)
II - RED. PUNKTE & brute force Suche	3m 6s	25	10.91	(5.33, 220.55, -0.05)
III - alle Punkte & $k$D-Baum	6s	27	8.24	(4.53, 221.00, -0.06)
IV - REDUZIERTE PUNKTE & $k$D-Baum	$<$2s	25	10.91	(5.33, 220.55, -0.05)

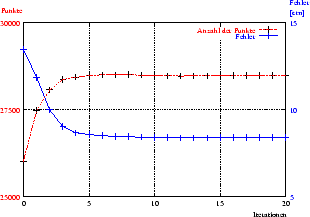
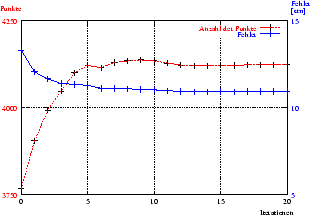
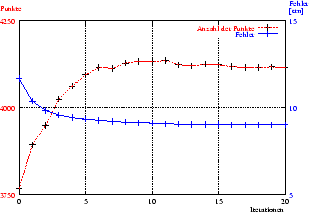
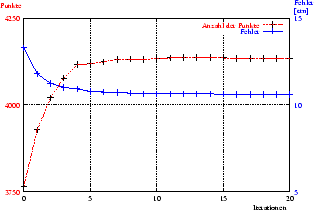
Abbildung 3.5 veranschaulicht die Entwicklung des mittleren Fehlers und die Anzahl der gepaarten Punkte in den ersten 20 Iterationen des Algorithmus. Die linke Abbildung zeigt die Entwicklung, falls alle Punkte Berücksichtigung finden, während in der rechten Abbildung nur die reduzierten Punkte einbezogen werden. Zu erkennen ist, dass beide Verfahren etwa gleich schnell konvergieren (in zirka 5 Schritten).

Abbildung: Die Entwicklung des mittleren Fehlers und die Anzahl der Punktpaare während des ICP-Algorithmus. Links: Methode I bzw. III. Rechts: Methode II bzw. IV.

Für die bisher präsentierten Ergebnisse wird wie beschrieben ein harter Schwellenwert verwendet und alle Punktpaare werden gleich gewichtet. Der Parameter $w_{i,j}$ ermöglicht allerdings auch eine Gewichtung der Punktpaare; die vorgestellte Transformationsbestimmung (Kapitel 3.3.3) wird dadurch nicht beeinflusst [40]. Neben der konstanten Verteilung der Gewichte erscheinen folgende Strategien logisch:

• Die Zuweisung von geringeren Gewichten zu Paaren mit größerem Punkt-Punkt Abstand. Dies ist vergleichbar mit der harten Schwellenwertmethode, allerdings werden Diskontinuitäten vermieden. Folgende Gewichte sind für den nächsten Test gewählt:
  $$w_{i,j} = \left\{ \begin{array}{ccl} & 1 - \frac{\left\lver... ...\mathbf{m}_i$\ ist}\\ & 0 &\mbox{sonst.} \end{array}\right.$$
  $d_{max}$ wurde wieder auf 25cm festgelegt.
• Große Gewichte werden Paaren zugewiesen, deren Remissionswert sich kaum unterscheidet. Sind nämlich die Intensitätswerte der Punkte annähernd gleich, ist es wahrscheinlicher, dass es sich um den gleichen Punkt handelt. $I(\mathbf{p})$ bezeichnet die Intensität eines Datenpunktes $\mathbf{p}$ . Folgende Formel wird verwendet:
  

  $$w_{i,j} = \left\{ \begin{array}{cll} = & 1 - \lvert{I(\mathbf... ...\mathbf{m}_i$\ ist,}\\ = & 0 &\mbox{sonst.} \end{array}\right.$$

  
  

Tabelle 3.2: Vergleich der Methoden zur Bildung von Punktpaaren (Forts.); Ausgangsposition des ICP-Algorithmus ist die auf Odometrie-Daten beruhende Roboterposition $(x,y,\theta) = (27.10,\ 233.20,\ 6.64)$; Zeiten bei brute-force Suche.

Methode	Zeit	Iterationen	Fehler	Endkoordinaten
IVa - RED. PUNKTE & dynamische Gewichte	$<$2s	25	9.0	(5.10, 221.38, -0.31)
IVb - RED. PUNKTE & Intensität	$<$2s	27	10.61	(6.14, 220.43, 0.51)

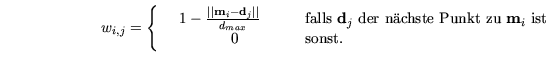
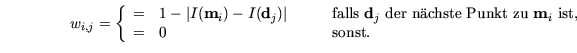Die Benutzung von dynamischen Gewichten und die Verteilung der Gewichte mittels Intensitätswerten lassen sich auch mit $k$d-Bäumen kombinieren, wobei die Programmlaufzeit dann ebenfalls zirka 2 Sekunden beträgt (vgl. Tabelle 3.2). Abbildung 3.6 zeigt die Entwicklung des mittleren Fehlers und die Anzahl der benutzten Punktpaare für diese beiden Strategien. Wie man sieht, wird das Fehlerminimum wiederum während der ersten Iterationen erreicht.

Abbildung: Die Entwicklung des mittleren Fehlers und die Anzahl der Punktpaare während des ICP-Algorithmus (Forts.). Links: Methode IVa. Rechts: Methode IVb.

Die angegebenen Endkoordinaten des Roboters können nicht mit einem Referenzwert verglichen werden, da die genaue Position des Roboters nicht bekannt ist. Der angegebene Fehler ist der Fehler $E(\MR,\mathbf{t})$ (3.7) und nicht jener der Roboterposition.