

Next: Kollisionsvermeidung.
Up: Das Anfahren der optimalen
Previous: Das kinematische Modell.
Der letzte Abschnitt beschreibt die
Kinematik des Robotersystems. Damit der Roboter wirklich Fahren kann,
ist seine Dynamik zu berücksichtigen. Aus der berechneten
Geschwindigkeit 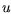 und der zu fahrenden Krümmung
und der zu fahrenden Krümmung 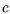 werden die
Motorwerte ermittelt. Zuerst bestimmt man dazu mittels Formel
(4.2) die Winkelgeschwindigkeit
werden die
Motorwerte ermittelt. Zuerst bestimmt man dazu mittels Formel
(4.2) die Winkelgeschwindigkeit 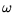 , um daraus
anschließend Werte für den rechten und linken Motor zu
generieren. Diese sind eventuell zu skalieren und ein Integrator
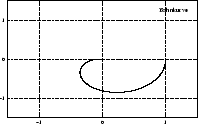
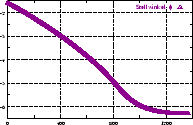
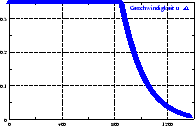
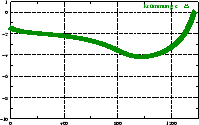
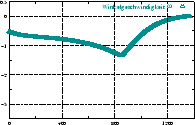
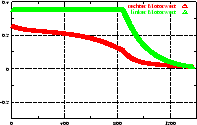
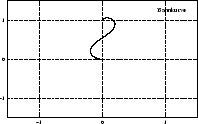
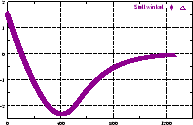
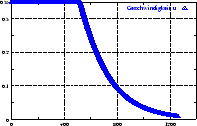
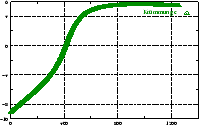
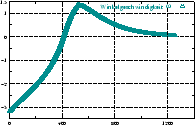
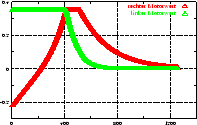
berücksichtigt die Trägheit des Roboters. Abbildung
4.12 zeigt den zeitlichen Verlauf der Werte
, um daraus
anschließend Werte für den rechten und linken Motor zu
generieren. Diese sind eventuell zu skalieren und ein Integrator
berücksichtigt die Trägheit des Roboters. Abbildung
4.12 zeigt den zeitlichen Verlauf der Werte 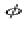 (Stellwinkel),
(Stellwinkel), 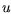 (Geschwindigkeit),
(Geschwindigkeit), 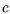 (Krümmung),
(Krümmung),
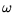 (Winkelgeschwindigkeit) und die daraus resultierenden Werte
für die Motoren an zwei Beispielen. Anhang B.3 zeigt die
Implementierung, die zu diesen Kurven führt.
(Winkelgeschwindigkeit) und die daraus resultierenden Werte
für die Motoren an zwei Beispielen. Anhang B.3 zeigt die
Implementierung, die zu diesen Kurven führt.



Next: Kollisionsvermeidung.
Up: Das Anfahren der optimalen
Previous: Das kinematische Modell.
Andreas Nüchter
2002-07-10