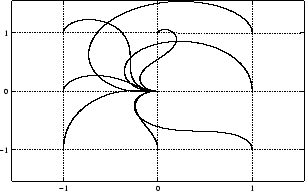


Next: Dynamik des Systems.
Up: Das Anfahren der optimalen
Previous: Das Anfahren der optimalen
Dem Controller liegt ein
kinematisches Modell zu Grunde, das in kartesischen Koordinaten
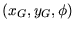 angegeben wird (vgl. Abbildung 4.9):
angegeben wird (vgl. Abbildung 4.9):
Dabei ist 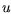 die Geschwindigkeit,
die Geschwindigkeit, 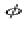 der Stellwinkel,
der Stellwinkel, 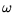 die Winkelgeschwindigkeit,
die Winkelgeschwindigkeit, 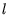 die Länge des Roboters,
die Länge des Roboters,
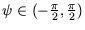 der Lenkwinkel und
der Lenkwinkel und 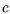 die Krümmung
der Trajektorie. Bei dem verwendeten Roboter spielt der Lenkwinkel
keine Rolle, da er einen Differentialantrieb, also zwei getrennt
ansteuerbare Antriebsräder besitzt und sich daher auf der Stelle
drehen kann.
die Krümmung
der Trajektorie. Bei dem verwendeten Roboter spielt der Lenkwinkel
keine Rolle, da er einen Differentialantrieb, also zwei getrennt
ansteuerbare Antriebsräder besitzt und sich daher auf der Stelle
drehen kann.
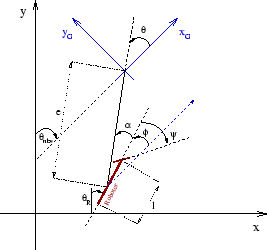
Das Modell (4.2) wird mit den polaren Zustandsvariablen
(vgl. Abbildung 4.9)
zu dem Zustandsraum
Abbildung 4.9:
Das kinematische Modell: Das lokale Koordinatensystem
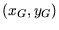 des verwendeten Controllers.
des verwendeten Controllers.
|
|
Dieser Zustandsraum ist vollständig definiert, außer für die Menge
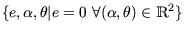 .
Das Problem besteht nun darin, glatte Funktionen für
.
Das Problem besteht nun darin, glatte Funktionen für 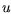 und
und
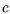 zu finden, die den Zustandsraum für jede anfängliche
Konfiguration
zu finden, die den Zustandsraum für jede anfängliche
Konfiguration
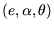 in das Ziel
in das Ziel 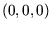 überführen
[46].
überführen
[46].
Bevor mit der Lösung dieses Kontrollproblems begonnen werden kann,
müssen die Pose des Roboters
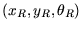 und die der
optimalen nächsten Scanposition
und die der
optimalen nächsten Scanposition
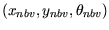 , die
im globalen Koordinatensystem bestimmt sind, in das Modell mit dem
Koordinatensystem
, die
im globalen Koordinatensystem bestimmt sind, in das Modell mit dem
Koordinatensystem
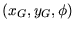 überführt werden (vgl. Abbildung
4.10). Die Gleichungen
überführt werden (vgl. Abbildung
4.10). Die Gleichungen
bewirken die gewünschte Koordinatentransformation.
Abbildung 4.10:
Einbettung der lokalen Motorcontroller-Koordinaten in das globale Koordinatensystem des Roboters.
|
|
G. Indiveri wählt folgenden Ansatz für die Lösung des Kontrollproblems
[46]: Da die Ableitungen der Zustände in (4.3)
für 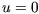 gleich Null sind und weil der Roboter nur vorwärts fahren
soll, bietet sich die Gleichung
gleich Null sind und weil der Roboter nur vorwärts fahren
soll, bietet sich die Gleichung
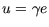 mit mit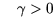 |
|
|
(4.7) |
als Lösung an. Mit diesem Ansatz und unter Verwendung der quadratischen
Lyapunov Funktion ergibt sich eine Lösung für 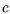 :
:
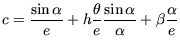 mit mit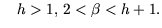 |
|
|
(4.8) |
Die beiden Formeln (4.7) und (4.8) beschreiben
den glatten Übergang des Zustandsraumes. Die genaue Herleitung der
Formeln befindet sich in Anhang A.5. Bei der
Implementierung muss dafür gesorgt werden, dass sich 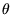 und
und
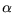 im Bereich von
im Bereich von
![$ [-2\pi,2\pi]$](img371.gif) befinden, damit sich für
befinden, damit sich für 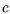 eine stetige Lösung ergibt. Die wesentliche Funktion des Controllers
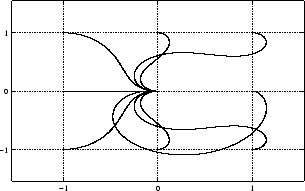
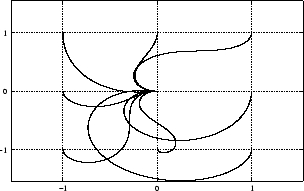
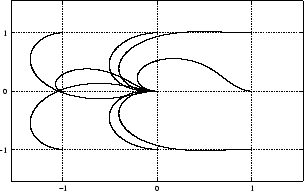
befindet sich in Anhang B.3. Abbildung 4.11
zeigt einige Bahnkurven des Controllers. Es ist ersichtlich, dass
jede gegebene Pose
eine stetige Lösung ergibt. Die wesentliche Funktion des Controllers
befindet sich in Anhang B.3. Abbildung 4.11
zeigt einige Bahnkurven des Controllers. Es ist ersichtlich, dass
jede gegebene Pose
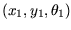 in eine andere
in eine andere
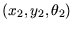 überführt werden kann.
überführt werden kann.



Next: Dynamik des Systems.
Up: Das Anfahren der optimalen
Previous: Das Anfahren der optimalen
Andreas Nüchter
2002-07-10
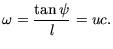
![]() .
Das Problem besteht nun darin, glatte Funktionen für
.
Das Problem besteht nun darin, glatte Funktionen für ![]() und
und
![]() zu finden, die den Zustandsraum für jede anfängliche
Konfiguration
zu finden, die den Zustandsraum für jede anfängliche
Konfiguration
![]() in das Ziel
in das Ziel ![]() überführen
[46].
überführen
[46].
![]() und die der
optimalen nächsten Scanposition
und die der
optimalen nächsten Scanposition
![]() , die
im globalen Koordinatensystem bestimmt sind, in das Modell mit dem
Koordinatensystem
, die
im globalen Koordinatensystem bestimmt sind, in das Modell mit dem
Koordinatensystem
![]() überführt werden (vgl. Abbildung
4.10). Die Gleichungen
überführt werden (vgl. Abbildung
4.10). Die Gleichungen
![]() gleich Null sind und weil der Roboter nur vorwärts fahren
soll, bietet sich die Gleichung
gleich Null sind und weil der Roboter nur vorwärts fahren
soll, bietet sich die Gleichung