Die Lösung für das Kontrollproblem aus Abschnitt 4.4 soll
hergeleitet werden. Setzt man den Ansatz
![]() mit
mit![]() (Formel (4.7)) in die Zustandsvariablen
(Formel (4.7)) in die Zustandsvariablen
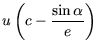 |
|||
Das obige gewöhnliche Differentialgleichungssystem ist über die
Position
![]() rückgekoppelt und wird durch den Roboter
gelöst. Die Fahrt des Roboters entspricht einer Simulation und damit
auch der Lösung des Systems. Die verbleibende Aufgabe besteht darin,
für die Konstante
rückgekoppelt und wird durch den Roboter
gelöst. Die Fahrt des Roboters entspricht einer Simulation und damit
auch der Lösung des Systems. Die verbleibende Aufgabe besteht darin,
für die Konstante ![]() , die zu fahrende Krümmung, einen Term zu finden,
so dass garantiert werden kann, dass die Null-Lösung
, die zu fahrende Krümmung, einen Term zu finden,
so dass garantiert werden kann, dass die Null-Lösung ![]() stabil
ist. Zusätzlich soll sich das System dieser Konfiguration
kontinuierlich annähern [46]. Eine solche
Stabilisierung von dynamischen Systemen durch Rückkopplung stellt eine
der wesentlichen Aufgaben der Steuerungstheorie dar.
stabil
ist. Zusätzlich soll sich das System dieser Konfiguration
kontinuierlich annähern [46]. Eine solche
Stabilisierung von dynamischen Systemen durch Rückkopplung stellt eine
der wesentlichen Aufgaben der Steuerungstheorie dar.
Die Null-Lösung heißt stabil, wenn es zu jedem
![]() ein
ein
![]() gibt, das nicht von der Zeit
gibt, das nicht von der Zeit ![]() , sondern nur von
, sondern nur von
![]() abhängt, so dass für jede Anfangskonfiguration kleiner
abhängt, so dass für jede Anfangskonfiguration kleiner
![]() die Lösung der Differentialgleichung auf die ganze positive
Halbachse
die Lösung der Differentialgleichung auf die ganze positive
Halbachse ![]() fortsetzbar und für alle
fortsetzbar und für alle ![]() diese Lösung
kleiner als
diese Lösung
kleiner als
![]() ist (vgl. Abbildung A.8)
[6].
ist (vgl. Abbildung A.8)
[6].
Ist das zu lösende Differentialgleichungssystem linear, beispielsweise
![]() , gibt folgender Satz Auskunft über die Stabilität
der Null-Lösung.
, gibt folgender Satz Auskunft über die Stabilität
der Null-Lösung.
Beweis:Siehe [6].![]()
Offensichtlich ist das Differentialgleichungssystem (A.21)
nicht linear. Im nichtlinearen Fall kann die Methode von Lyapunov für
den Stabilitätsnachweis verwendet werden. Die Lyapunov Funktion ist
eine skalare Funktion ![]() , definiert über einer verbundenen Region
, definiert über einer verbundenen Region
![]() , die den Nullpunkt enthält. Sie ist darüber hinaus positiv
definit, d.h. es gilt
, die den Nullpunkt enthält. Sie ist darüber hinaus positiv
definit, d.h. es gilt
![]() und
und
![]() für alle
für alle
![]() . Weiterhin sind ihre ersten
partiellen Ableitungen an jedem Punkt von
. Weiterhin sind ihre ersten
partiellen Ableitungen an jedem Punkt von ![]() stetig. Die Ableitung
von
stetig. Die Ableitung
von ![]() für ein beliebiges System
für ein beliebiges System
![]() wird mit
wird mit
![]() bezeichnet und ist definiert als das Skalarporodukt
bezeichnet und ist definiert als das Skalarporodukt
In physikalischen Systemen lässt sich die Stabilität durch die Betrachtung der Gesamtenergie nachweisen. Bleibt diese Energie gleich oder sinkt sie, ist die Stabilität sofort klar. Die Gesamtenergiefunktion ist dann die Lyapunov Funktion [37]. Die Bestimmung einer Energiefunktion erfordert in der Regel die Lösung des vorliegenden Differentialgleichungssystems. Ist nur die Stabilität von Interesse, versucht man eine Lyapunov Funktion zu raten.
Die nun folgende Rechnung zeigt, dass eine Lyapunov Kandidatenfunktion
bei geeigneter Wahl von ![]() die Stabilität der Lösung von
(A.21) garantiert. Weiterhin werden die auftretenden Grenzwerte
nachgewiesen und unter anderem folgender kleiner Hilfssatz benutzt:
die Stabilität der Lösung von
(A.21) garantiert. Weiterhin werden die auftretenden Grenzwerte
nachgewiesen und unter anderem folgender kleiner Hilfssatz benutzt:
Die quadratische Lyapunov Kandidatenfunktion
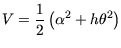 mit mit |
Durch diese Überlegungen ist das Kontrollgesetz (4.7) und
(A.22) nachgewiesen. Das Verhalten hängt von den Parametern
![]() und
und ![]() ab.
ab. ![]() hat einen endlichen Wert, solange
hat einen endlichen Wert, solange ![]() und
und ![]() endlich sind. Auch die Winkelgeschwindigkeit
endlich sind. Auch die Winkelgeschwindigkeit ![]() muss begrenzt sein. Dazu analysiert man
muss begrenzt sein. Dazu analysiert man
![]() . Wenn
. Wenn ![]() gegen Null geht, können die
Zustandsgleichungen aus (A.24) durch folgendes lineare System
approximiert werden:
gegen Null geht, können die
Zustandsgleichungen aus (A.24) durch folgendes lineare System
approximiert werden:
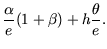 |
Im oben hergeleiteten Kontrollgesetz für ![]() (4.7) und
(4.7) und ![]() (4.8) ist die Geschwindigkeit abhängig vom Abstand. Da
jedes Fahrzeug eine maximale Geschwindigkeit
(4.8) ist die Geschwindigkeit abhängig vom Abstand. Da
jedes Fahrzeug eine maximale Geschwindigkeit ![]() besitzt, tritt
in vielen Applikationen eine Sättigung auf, falls der Zielpunkt zu
weit entfernt ist. Demnach ist
besitzt, tritt
in vielen Applikationen eine Sättigung auf, falls der Zielpunkt zu
weit entfernt ist. Demnach ist
sat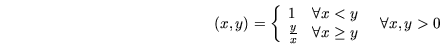 |
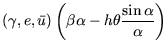 |
|||
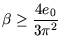 |