Model Refinement

Due to unprecise measurements or registration errors, the 3D data might be erroneous. These errors lead to inaccurate 3D models. The semantic interpretation enables us to refine the model. The planes are adjusted such that they explain the 3D data, and the semantic constraints like parallelism or orthogonality are enforced.

To enforce the semantic constraints, the model is first simplified. A preprocessing step merges neighboring planes with equal labels, e.g., two ceiling planes. This simplification process increases the point to plane distance, which has to be reduced in the following main optimization process. This optimization uses an error function to enforce the parallelism or orthogonality constraints. The error function consists of two parts. The first part accumulates the point to plane distances and the second part accumulates the angle differences given through the constraints. The error function has the following form:

$$\vspace*{-1mm} E(P)$$ (5)

$$end{tex2html_deferred}! = $$ (6)

$$end{tex2html_deferred}!$$ (7)

$$end{tex2html_deferred}! \sum_{p_i \in P} \sum_{\V x \in p_1}$$ (8)

$$end{tex2html_deferred}!$$ (9)

$$end{tex2html_deferred}! \norm { (\V x - {\V p_i}_1) \cdot \V n_i }$$

$$end{tex2html_deferred}$$ (10)

$$end{tex2html_deferred} + ~~ \gamma$$ (11)

$$end{tex2html_deferred}!$$ (12)

$$end{tex2html_deferred}! \sum_{p_i \in P} \sum_{p_j \in P} c_{i,j}, \vspace*{-1mm}$$ (13)

where $c_{i,j}$ expresses the parallelism or orthogonality constraints, respectively, according to

$$\begin{array}{lll@{}l} c_{i,j} & = & \min\{ & \vert \arcco... ...n_j) \vert, \mbox{~~respectively.}} \vspace*{-1mm} \end{array}$$

Minimization of $E(P)$ (eq. (3)) is a nonlinear optimization process.

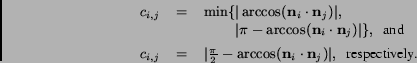
The time consumed for optimizing $E(P)$ increases with the number of plane parameters. To speed up the process, the normal vectors $\V n$ of the planes are specified by spherical coordinates, i.e., two angles $\alpha, \beta$. The point $\V p_1$ of a plane is reduced to a fixed vector pointing from the origin of the coordinate system in the direction of $\V p_1$ and its distance $d$. The minimal description of all planes $P$ consists of the concatenation of $p_i$, with $p_i = (\alpha_i, \beta_i, d_i)$, i.e., a plane $p_i$ is defined by two angles and a distance.